Yazı tura oyununun rastlantısal sonuçları üzerine ne yapacağımıza karar verdiğimiz durumları birçoğumuz muhakkak yaşadık. Sinemaya veya yüzme havuzuna gitme konusunda kararsız kalan iki arkadaş, ne yapacaklarını madeni bir paranın inisiyatifine bırakabilir! Yazı gelirse sinema ya da tura gelirse yüzme havuzu. Peki, gerçekten madeni paranın yazı veya tura gelecek olması tamamen rastlantısal mı, yoksa gerekli hesaplamalarla doğru tahmin edilebilir mi? Aslında Klasik mekanik yasaları olarak adlandırdığımız fizik yasaları bu durumu net bir şekilde tahmin edebilir. Hatta doğa yasalarını barındıran algoritmalar yazarak sonucu bir bilgisayar programına bile tahmin ettirebiliriz.
Klasik mekanik yasaları bir parçacığa etki eden kuvvetin, parçacığın hız, belirli bir zaman sonra konumu, enerjisi, momentumu ve torku gibi fiziksel özelliklerin ne olduğuna dair nicel söylemlerde bulunur. Bunu yaparken de bir kesinlik belirtir. Eğer yazı tura oyununda, madeni paranın kütlesini, ona fırlatırken uyguladığımız kuvvet, paranın atıldığı yerdeki kütle çekimi ivmesi, o andaki hava sıcaklığı varsa rüzgâr ve paranın hangi mesafede yakalanacağı değerleri ile paranın dönme frekansı hesaplanabilirse, henüz parayı atmadan sonucun ne olacağını bilebiliriz. Bu klasik fiziğin makro evreni anlama konusunda bizlere sunduğu bir özelliktir. Bugün bu sayede uzay araçları sorunsuz bir şekilde uzaya fırlatılabiliyor ve neredeyse kusursuza yakın hava durumu tahminlerinde bulunulabiliyor. Klasik mekanik yasaları şu anda durumunu bildiğimiz bir nesnenin daha önce nerede ne yapıyor olduğunu ve daha sonra nerede ne yapacak olduğu hakkında kesin tahminlerde bulunmamızı sağlar.
1900 yılına gelindiğinde klasik mekanik yasaları için yolunda gitmeyen bir şeyler olur. Isınan bir cismin yaptığı ışınımın anlamlandırılması konusunda klasik mekaniğin tanımladığı enerji ifadeleri yetersiz kalır. Bugün mor ötesi felaket olarak adlandırılan olay klasik mekaniksel yaklaşım terkedilerek Planck tarafından aşılmıştır. Planck’a göre ışınımım enerjisini kuantalar olarak düşünüldüğünde sonuçlar deneysel gözlemlerle uyum içinde olmaktadır. Bu sayede kesintisiz olan enerji, hız, konum ve momentum gibi fiziksel özellikler artık kesikli-belirli değerlerde bulunabilen durumlardadır. Yani kuantumsal bir yapıda olduğu anlaşılmıştır. Ancak burada siz değerli okuyucuların dikkat etmesi gereken bir nokta vardır. Işınımın anlaşılması için klasik yaklaşımdan, kuantalaşmış yaklaşıma geçiş, kuantum mekaniğinin kapısını aralasa da, bu klasik mekaniğin artık saf dışı olduğu anlamına gelmez. Atom ve atom altı parçacıkların, fotonların anlaşılması için kuantumsal yaklaşım ne kadar doğru ise, algılanabilir dünyada gerçekleşen mekanik olayların klasik mekanik yaklaşımları ile anlaşılması aynı doğrulukla devam etmektedir. Kuantum mekaniksel söylemlerde, gündelik boyutlara geçtiğimizde klasik mekanik söylemleri ile uyum içindedir.
1900 yılından itibaren bu alanda çalışmalar artarak, kuantum mekaniğinin matematiksel temeli atılmış ve geliştirilmiştir. O dönemlerden bakıldığında matematiksel temelli bir model olarak görünse bile, bugün kuantum teknolojileri olarak adlandırdığımız alandan çıkan ürünler sayesinde kuantum mekaniğinin elle tutulabilir sonuçlarını görebiliyor ve bunlardan faydalanabiliyoruz.
Kuantum mekaniği yasaları klasik fizik yasalarından farklı olarak parçacıkların ölçülebilen özelliklerini (enerji, momentum, konum gibi) birer matematiksel işlemci olarak tanımlar. Evet, en ilginç nokta belki de budur. Şöyle ki, klasik mekanik yasalarınca bir cismin sahip olduğu mekanik enerji onun kinetik ve potansiyel enerjilerinin toplamından oluşur. Burada potansiyel kütle çekimi potansiyel enerjisi olabildiği gibi elektriksel potansiyel enerji de olabilir. Ancak kuantum mekaniği sınırları içerisine girdiğimizde toplam enerji tanımı aynı olmakla beraber eşitlikler değişir.
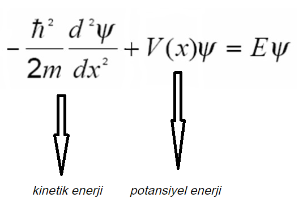
Bu eşitlik HΨ = EΨ formunda daha sade bir biçimde yazılabilir. Burada H, kuantum mekaniksel parçacığın sahip olduğu kinetik ve potansiyel enerjilerinin operatör karşılılarının matematiksel toplamıdır ve Hamiltonyen olarak adlandırılır. Bu hali ile bile masum durmayan bu denklem bir protonun etrafında dönen bir elektron için bile çözümü sayfalar sürmektedir. Eşitlikteki Ψ ise, bu diferansiyel denklemin çözümünü sağlayan fonksiyondur. Kuantum mekaniğinde bu fonksiyona dalga fonksiyonu denir. Kuantum mekaniksel parçacığın gözlenebilen tüm değerlerinin olasılıklar dahilinde bulunmasını sağlar. Kuantum mekaniği ile yakından ilgilenenler dalga fonksiyonundan elde edilen değerlere beklenen değer ismini vermişlerdir. Çözüm sonuçları bizlere elektronun bir bulut içinde gezdiğini dolayısıyla belirli bir zamandaki fiziksel özelliklerini net bir şekilde söylenemeyeceğini ancak tahmin edilebileceğini söyler. Aşağıdaki eşitlikte hidrojen atomundaki elektronun, ikinci kabukta ve z yönüne yönelmiş p orbitalindeki konumsal durumunu içeren dalga fonksiyonu görülmektedir.
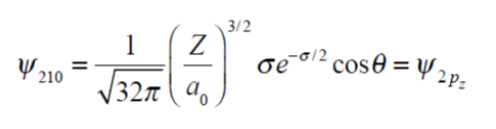
Yukarıdaki ilk eşitlik zamandan bağımsız Schrödinger denklemidir ve yalıtılmış bir hidrojen atomu için doğru sonuçlar vermektedir. Yine bu eşitlik hidrojen tipi yapıların çözülmesinde tam doğru olmamakla birlikte kabul edilebilir doğrulukta sonuçlar vermektedir. Bir elektronunu kaybetmiş hidrojen molekülü, iki elektronunu kaybetmiş lityum atomu ve nötr sodyum atomu hidrojen tipi yapılara örnek olarak verilebilir.
Saydığımız bu yapıların ilk ikisinde yörüngede dolanan bir elektron sodyumda ise son yörüngede bir elektron bulunmaktadır. Bu sebeple bunlara hidrojen tipi yapılar denmektedir. Ancak bir elektronunu kaybetmiş hidrojen molekülünde bile potansiyel kısma ilave terimler gelmektedir. Örnek olarak bu terimler Hidrojen molekülündeki elektronun birinci ve ikinci proton ile etkileşme enerjisi ve iki protonun kendi içinde etkileşme enerjisidir. Bu sayı lityum +2 iyonuna söz konusu olduğunda çekirdekteki bulunan proton sayısı sebebiyle daha çok artmaktadır. Sodyum atomunda ise bu eklere ilave olarak perdeleme denilen ekstra bir terim girmektedir. Çünkü son yörüngede dolanan elektron çekirdekte bulunan protonları zayıf görmektedir. Dolayısıyla bu etkileşim enerjisinde farklılıklar meydana getirmektedir. Ancak doğada sadece hidrojen atomu bulunmamaktadır. Sistemin sahip olduğu parçacıkların sayısı arttıkça bu parçacıklar arasındaki etkileşim sayısı da artmaktadır ve her bir etkileşim bir terim olarak yukarıda gösterdiğimiz toplam hamiltonyene bir terim ilave eder.
Buradan çıkarılan sonuç parçacık sayısı ile birlikte etkileşim sayısının artmasıdır. Bu nedenle hamiltonyendeki etkileşmeyi temsil eden terim sayısı artırmakta bu da çözümü oldukça zorlaştırmaktadır. Tam da burada çözümlerde bazı yaklaşımlar veya kabuller yapılmaktadır. Birazdan örneklerini vereceğimiz kabullerin yapılması durumunda dahi Moleküler simülasyonları yapan programlar daha büyük moleküllerin analizinde işlem gücü açısından zorlanmaktadır.
Çekirdek ve Elektron Hareketi
1927 yılında Max Born ve J. Robert Oppenheimer isimli iki fizikçi tarafından bir kabul öne sürülmüştür. Bu öneriye göre moleküllerdeki çekirdeğin ve elektronun hareketi ayrı ayrı ele alınabilir. Bu varsayıma göre hamiltonyendeki terimlerde bir azalma ve çözüme daha da yaklaşma gerçekleştirilmiştir. Bir başka yaklaşım da Hartre focke yöntemidir. Bu yöntemde bir elektronun etkileşimi hesaplanarak, diğerlerinin ortalama etkisi dikkate alınır. Her iki yöntemde de hamiltonyendeki terim sayısı azalmakta ve gerçek değere daha çok yaklaşılmaktadır. Ancak yine de gerçek değerlere ulaşma konusunda zayıftır.
Şimdi siz değerli okuyucuların soracağı soru; “Moleküler sistemleri tam olarak çözebilirsek ne olur?” sorusudur. Eğer moleküler sistemler nicel olarak iyi anlaşılırsa; yani taban ve uyarılmış durum enerjileri net hesaplanır, moleküler orbitaller doğru şekilde tanımlanırsa, hesaplamalı kimya alanında devasa bir çağın kapısını aralanır ve insanoğluna yansıması son derece faydalı olur. Günümüzde bu alanda oldukça iyi simülasyon çalışmaları yapılmaktadır.
DNA gibi büyük moleküllerin yapısı anlaşılarak bu sayede kusur olarak tanımlanan kısımlara müdahale edilebilir. Etik değeri tartışılmakla beraber yapı üzerinde modifiyeler gerçekleştirilebilir. Genetik hastalıkların önüne geçilebilir.
İlaç sektöründe kişiye özel ilaçların tasarımı hızlanırken, ilaçlardan alınan verimin maksimum seviyeye ulaşılması sağlanabilir.
Malzeme bilimi konusunda, yeni maddelerin sentezi labaratuvarlarda yapılan sayısız denemelerden geçmek zorunda kalmayarak, doğru simülasyonlarla elde edilen bilgi ışığında kaliteli ve verimli malzemeler yapılabilir.
Tabi tüm bunların gerçekleşebilmesi için bu hesapları yapabilen süper güçlü bilgisayarlara gerek duyulmaktadır. Her ne kadar bilgi işleme teknolojisi gelişmiş olsa da, devasa büyüklükteki verileri işleyecek, simülasyonlar yapan, sonuçlar çıkaran işlemler hala çok zaman almaktadır. Bu evlerimizde kullandığımız geleneksel bilgisayarların bilgiyi voltajlara kodlayıp sıra ile işleyebilmesinden kaynaklanmaktadır. Ancak Richard Feyman’ın 1981 tarihli, “simulating physics with computer” başlıklı makalesinde önerdiği gibi, doğa kuantum mekanikseldir ve kuantum mekaniği yasaları kullanılarak simüle edilebilir fikri, bu simülasyonların gelecekte inşa edilecek kuantum bilgisayarları ile yapılması zaman faktörünü minimuma indireceği gibi daha doğru tahminler yapılmasına sebep olacaktır.
Bu işlemlerin kuantum bilgi işleme tekniği ile nasıl yapılabileceğini sunduğu devasa avantajları ile birlikte konu alan temel düzeyde bir yazıyı sizlerle bir sonraki yazıda paylaşmaktan çok mutlu olacağım.
Benzer içeriklerimize buradan ulaşabilirsiniz.
Yazar: Murat Kurt
Redaktör: Yasir Ölmez
Kaynak:
Feynman, R.P. Simulating physics with computers. Int J Theor Phys 21, 467–488 (1982).









