Geçtiğimiz gün kuantum teknolojileri alanında önemli isimlerden Jonathan Dowling’i 65 yaşında kaybettik. Kendisinden Onur Danacı ile yaptığımız Kuantum Teknolojileri Sohbetleri bölümünde de bahsetmiştik (konuşmanın o kısmı için tıklayabilirsiniz). Dowling’in doktora hocası olan Asım Orhan Barut’a ithafen ölümünden sonra yazdığı anma yazısınaysa buradan erişebilirsiniz (veya buradan). Bu yazıdaysa 2003 yılında Dowling ve Milburn tarafından kaleme alınan “Kuantum Teknolojisi: İkinci Kuantum Devrimi” üzerinden Dowling’in bizim camiaya mirası olan ‘kuantum teknolojisi’ kavramının literatüre girerken hangi temel fiziksel ilkeler üzerinden ele alındığına değineceğiz.
Daha önce Ruken tarafından kaleme alınan “Kuantum Teknolojiler ve Uygulama Alanları” yazısında bu konulara bir giriş yapmıştık. Hatırlamak için bakalım:
Kuantum Teknoloji Nedir?
Kuantum teknolojiler; fizik ve mühendislik dallarının bir araya gelmesiyle ortaya çıktı. Temel olarak, kuantum sistemlerin sunduğu (süperposizyon, dolanıklık gibi) farklı özelliklere dayanıyor. Klasik bilgisayarlarda veri işleme ve saklama ikili sisteme dayanır. Yani bir bit sadece iki durumdan birinde (1 ya da 0) olabilir. Kuantum fizikte geçen “Süperpozisyon” ise bir parçacığın kuantum durumunun aynı anda farklı durumlarda olabilmesi anlamına gelir.Yani “kubit” olarak adlandırılan kuantum bit, aynı anda hem 1 hem de 0 durumunda olabilir. Kuantum dolanıklık ise; iki benzer parçacığın aralarında fiziksel bir etkileşim olmadan bağlantılı olmasını ifade ediyor. Kuantum teknolojiler bu kavramlar üzerine kuruluyor.
Bu tanım genelde bizim QTurkey altında ele aldığımız teknolojileri kapsamak için yeterli olsa da Dowling ve Milburn’ün orijinal kuantum teknolojisi tanımlarına göre yetersiz kalıyor. Daha doğrusu bizim burada yaptığımız tanım kuantum bilişim teknolojisi (quantum information technology) diyebileceğimiz bir alanla sınırlı. Oysa 2003’teki makaleye göre kuantum teknolojisi denildiğinde çok daha geniş bir teknoloji kümesine gönderme yapılıyor.
Makalede öncelikli olarak kuantum teknolojilerinin dayandığı kendine özgü (klasik karşılığı olmayan) ilkeler altı başlıkta veriliyor.
- Kuantizasyon: Sıkıca kapatılmış parçacıklardan oluşan sistemlerin enerji seviyeleri sürekli değil kesiklidir. Örneğin, bir hidrojen atomunun çevresinde en düşük enerji seviyesinde dolanan elektronu oradan koparmak için 13.6 eV enerji gerekir. İkinci en düşük enerji seviyesinde dolanan elektronu koparmak içinse 3.4 eV enerji. Dolayısıyla bu enerji seviyeleri arasındaki geçişlerde 10.2 eV’lik bir enerji salınımı olur. Dedektörünüzde bunu gördüğünüzde “ikinci seviyede bir elektron birinci seviyeye düşmüş” diyebilirsiniz. Peki bu ne işimize yarar?
Normalde görünür ışığın tayfı aşağıdaki gibidir:

Elinizde bir malzeme var, neyden yapıldığını bilmiyorsunuz diyelim ve çeşitli deneyler sonucu (mesela malzemeyi ısıttınız ve enerji saçmasına izin verdiniz) aşağıdaki gibi bir tayf gözlemlediniz.

Eğer enerji seviyelerinin kuantizasyonundan habersiz olsaydınız yapmanız gereken şey gidip daha önce bilinen elementlerin salınım tayflarına bakıp karşılaştırma yapmak olurdu. Oysa şu an matematiksel olarak elinize gelen ışıkların renginden dalga boylarının kaç nanometre olduğunu çıkarıp oradan enerji seviyelerini bulup sonra bunları Schrödinger denkleminin farklı elementler için olan çözüm sonuçlarıyla karşılaştırıp elinizdeki malzemenin hangi elementlerden oluştuğunu bulabilirdiniz! Elbette genelde bu kadar basit sistemlerle karşılaşmak zor. Ama tarihsel olarak değerli bir örnek olarak 1800lerde Alman fizikçi Joseph von Fraunhofer tarafından geliştirilen ve astronomik gözlemlere dayanan aşağıdaki tayfın açıklanması buna dayanır.
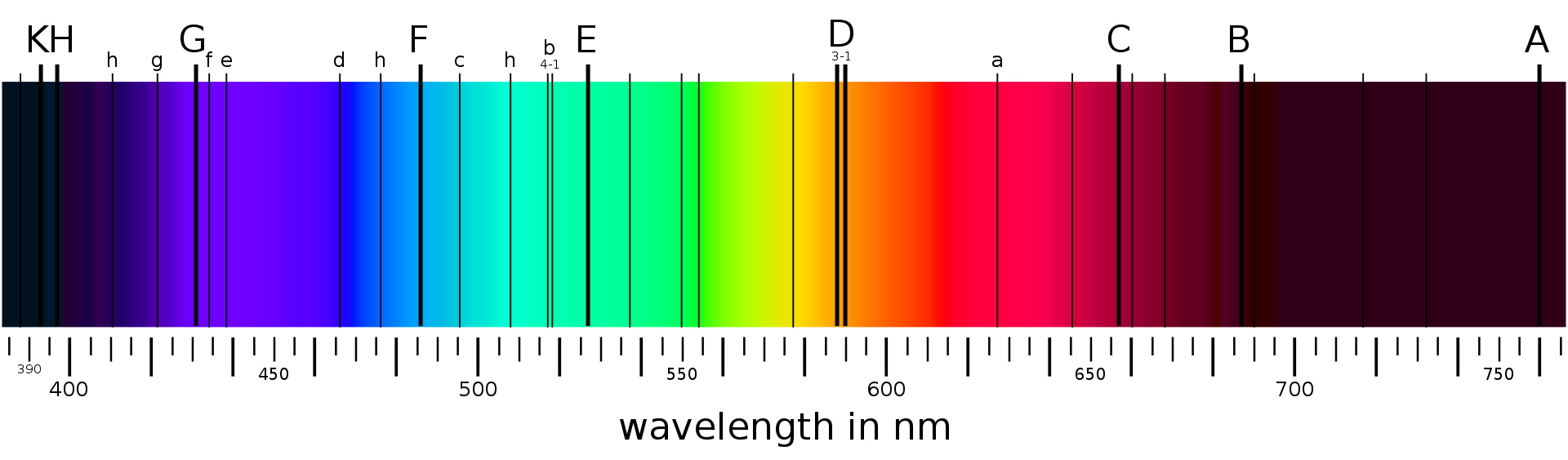
Yukarıda gördüğünüz harflerin hangi elementlere tekabül ettiğine dair aşağıdaki tabloyu kullanmak size, sırf dünyadan bakarak bir yıldızın hangi elementlerden oluştuğunu anlamanız konusunda bir imkan sunmaktadır. Aralarında ise 100 yıldan uzun bir süre var. Yani 100 yıl boyunca spektroskopi kullanan bilim insanları “bu çizgi şu elementikiyle uyuşuyor” şeklinde, tamamen deneysel tablolara dayanan teorisiz gözlemlerle bilimlerini icra etmek durumundaydılar. Oysa bugün lise düzeyinde bile çözülebilecek bir matematiksel denklemle bunların hepsini kağıt kalem ve birkaç tablo kullanarak yapabiliyoruz. İşte bu, enerjinin kuantizasyonu anlamanın faydalarından yalnızca birisi!
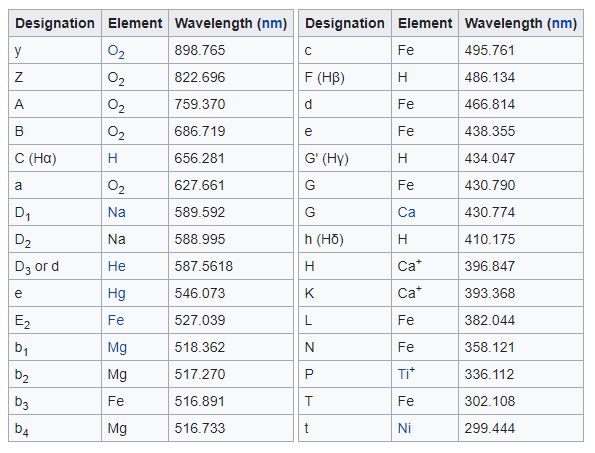
- Belirsizlik ilkesi: Düzgün bir kuantum durumun sonuçlarından kesin olabileceğimiz her ölçülebilir fiziksel niceliği için en az bir diğer fiziksel niceliğin sonuçları rastgele olacaktır. Bu da klasik bir karşılığı olmayan fiziksel fenomenlerden birisidir. Genel verilen örnek parçacıkların pozisyonu ve momentumudur. Bir parçacığın tam olarak nerede olduğunu biliyorsanız bir sonraki an nerede olacağını bilemezsiniz, aynı şekilde bir parçacığın momentumunu tam olarak biliyorsanız o parçacığın pozisyonunu bilemezsiniz. Peki belirsizlik ilkesi ne işimize yarar?
Buna daha yakın bir örnekle yanıt verelim, kuantum rastsal sayı üreteçleri.

Samsung Mayıs ayında ‘Galaxy A Quantum’ isimli telefonunu piyasaya tanıttı. Daha önce 2018 tarihli “Kuantum Teknolojileri: Dünyada Neler Oluyor?” başlıklı raporumuzda SK Telekom’un İsviçreli kuantum kriptografi firması IDQ’yu bir nevi bünyesine kattığından bahsetmiştik. Şimdi de SKT ve Samsung, IDQ’nun kuantum rastsal sayı üreteçlerini minyatürleştirip çip haline getirerek ticari bir telefonun içinde satışa çıkardı. Öyle ki, telefonun adına bile “Quantum” diye ekleyerek reklam malzemesi yaptılar. Bunun belirsizlik ilkesiyle ilgisiyse şurada yatıyor, klasik fiziksel sistemlerde rastgelelik üretmek çok zor, rastgelelik ise kriptografi için önemli bir ‘kaynak’.
Teknik detaylara girmeden şu şekilde özetleyebiliriz, elinizdeki sistemde ürettiğiniz fotonların bir özelliğini ölçtüğünüzü düşünün. Artık bu fotonun bir niceliğini tam olarak biliyorsunuz, bu da bir başka niceliğini tamamen belirsiz — yani rastgele kılıyor. Sonrasında bu rastgele nicelik üzerine ölçüm yapıp bunları kaydediyorsunuz ve artık elinizde tamamen rastgele bir kriptografik anahtar var, yani bu anahtarla şifrelediğiniz bir veriyi yalnızca bu anahtarla okuyabilirsiniz (elbette karşı tarafa iletim konusu da var, bunun için de süperpozisyonu kullanacağız, ama o başka yazının konusu).

Bu arada değinmeden geçmemek lazım ki Türkiye’de de kuantum rastsal sayı üreteçleri üzerine çalışmalar yapılmış ve TÜBİTAK’ın böyle bir ürünü bile bulunmakta. Ama elbette IDQ’nun ve SKT’nin buradaki gerçek başarısı 8 cm x 8 cm x 15 cm olan bu koca sistemi alıp 2.5 mm x 2.5 mm’lik bir ince chipset’e minyatürize etmek.
- Kuantum Süperpozisyon: Bir kuantum sistem birbirinden ayırt edilebilir en az iki duruma sahipse (yukarıdaki elektron örneği gibi, ya en düşük enerji düzeyinde ya birinci enerji düzeyi) bu sistem iki sistemin bir süperpozisyonu halinde de bulunabilir.
Daha önce bu konuyu Kutlu’nun “Kuantum Süperpozisyon ve Çift Yarık Deneyi Nedir?” yazısında ele almıştık. O nedenle üzerinden geçmeyeceğiz. Ancak ilgilileri için kuantum süperpozisyonun fotonik sistemlerde ve optik elemanlarla nasıl “klasik fizikle çelişen” sonuçlar veren bir fiziksel fenomen olduğunu kaliteli bir şekilde açıklayan quantum game with photons oyununu tavsiye ederiz. Başka bir örnek olarak süperpozisyonun atomik (sezyum) saatlerde kullanımı üzerine bilgiye buradan erişebilirsiniz. Bu atomik saatler ise gündelik hayatta hemen her gün işimize yarayan bir teknolojiyi mümkün kılan hassas zaman ölçümlerinde kullanılıyorlar — GPS!

Özel görelilik kuramı bize birbirlerine göre farklı hızlarda hareket eden fiziksel sistemlerde yapılan pozisyon ve zaman ölçümlerinin farklı olduğunu söylüyor. Saatte 5 km hızla giden bir bisiklette gördüğünüz 1 metre uzunluk saatte 1005 km hızla giden uçaktaki birisi için 1 metre olarak görünmeyecektir. O zaman her şey görecelidir değil mi, sonuçta kuramın adı da buradan geliyor değil mi? Aslında hem evet hem hayır, aşağıda gördüğünüz ‘Lorentz dönüşümleri’ sayesinde bu iki fiziksel referans sistemi arasında geçiş yapabiliyoruz. İki sistem arasındaki göreceli hız farkı 1000 km/saat olacak, bu da yaklaşık saniyede 280 metre hıza tekabül ediyor. Yani formülde v = 280 m/s olacak.
Formüldeki c’nin (yani ışık hızının) saniyede 300.000.000 m/s saniye olduğunu düşünecek olursak sizin hissettiğiniz her 1 saniye için giden kişiye yaklaşık 0.999999999999 saniyeymiş gibi geleceğini görebilirsiniz. Saniyenin trilyonda biri kadar bir kayma. Yani ikinizde de birer saat olsa ve diğer kişi 16.000 yıl boyunca aralıksız olarak 1005 km/saat hızla giden bir uçakta durursa saatleriniz arası 1 saniyelik fark oluşacak. Ses hızına yakın uçan bir jeti 16.000 yıl boyunca aralıksız uçurursanız aradaki 1 saniyelik farkı görebileceksiniz! Peki bunu her gün her dakika hem de anlık olarak yapmak istiyorsanız? İşte o noktada, sıfırdan sonra en çok kaçıncı basamağı kesin olarak ölçebileceğiniz önemli hale geliyor. Bu da, atomik saatlerin ve hassas zaman ölçümlerinin gerekliliğini zorunlu kılıyor. Bunun için de, süperpozisyon fenomenini kullanarak sezyum atomlarının enerji salınımları ihtimallerini hesaplayabilmeniz gerekiyor.
Özel göreliliğe dair sezyum tabanlı atomik saatlerin uçaklarda gezdirilmesiyle yapılmış 1971 tarihli Hafele–Keating deneyini buradan inceleyebilirsiniz.
- Tünelleme: Kuantum parçacıklar klasik parçacıkların aksine daha geniş bir uzamsal dağılımları olmasından ötürü klasik fiziğe göre mümkün olmayan davranışları sergileyebilirler.
Kuantum sistemlerin uzamsal dağılımları üzerine “Kuantum Fiziğine Giriş: Sıfırdan Bire” yazımda detaylı bir giriş yapmıştım. Peki bunun kuantum tünelleme fenomeniyle ve bu fenomenin gündelik hayatımızla ne gibi bir ilişkisi bulunmakta?
Yukarıda gördüğünüz fotoğrafta E enerjiye sahip kuantum parçacığın bir sistemin yüksek bir potansiyel bariyerle karşılaştığında (V) olasılık dağılımını görüyorsunuz. Yazıyı okuyanların hatırlayacağı üzere bu genlikler olasılık genliği, yani parçacığın gerçekten orada olma ihtimali bu genliklerin karesi. Bu da kısaca şu demek, parçacığı solda görme ihtimalimiz tepe ve dipler için en yüksek, ancak parçacığı engelin sağında görme ihtimalimiz yine de var. Oysa klasik bir sistemde, örneğin bilardo topunu duvar attığımızda, eğer topun enerjisi duvarı kırmaya yetecek kadar yüksek değilse topun %100 ihtimalle geri sekmesini bekleriz. Kuantum parçacıklar ise, düşük de olsa, bir ihtimalle duvarın arkasında belirebiliyorlar. İşin ilginç kısmıysa parçacığı duvarın ‘içinde’ görme ihtimalimiz var gibi duruyor olmasına karşın aslında yok! Yani parçacığı ya duvarın solunda ya da sağında görüyoruz. Bu klasik bir parçacık olsaydı biz solda fırlattığımız için sadece solda görebilecektik.
Bu garip hikayenin bize klasik fizikle açıklanamayan sağladığı avantaj nedir diye soracak olursak gelen yanıtsa yine göklerde, Güneş’i anlamak, daha doğrusu tüm yıldızları, daha da doğrusu füzyon tepkimesini.
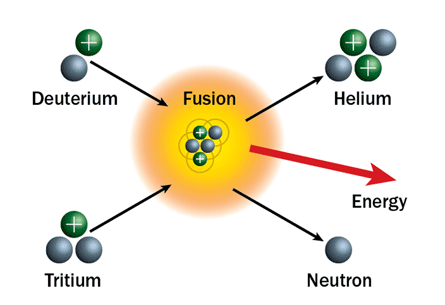
Hepiniz liseden hatırlarsınız, + yükler -’leri çeker diğer +’larıysa iter. Coulomb kuvveti dediğimiz bu çekme-itme ise aradaki mesafenin 1 bölü kareköküne bağlıdır. 1 birim uzaklıktaysanız 1 birim itiyorsa 2 birim uzaklıkta 0.25 birim iter, 5 birim uzaklıkta 0.04 birim iter. Peki ya 0.1 birim uzaktaysanız? O zaman 100 birim iter. Peki ya 0.01 birim, o zaman 10.000 birim iter! Dolayısıyla iki artı yüklü proton birbirine yaklaştıkça aralarındaki itme kuvveti üstel olarak artar ve bir araya gelecekleri zaman sonsuza gider. O zaman bu Hidrojen atomları nasıl oluyor da bir araya gelip Helyum atomunu oluşturabiliyor? İşte bunun yanıtı tünellemede yatıyor, çok düşük ihtimalle bazı protonlar potansiyel bariyerinin öte tarafında beliriyor ve eğer onları bir arada tutacak diğer kuvvetler sayesinde (güçlü nükleer kuvvet gibi) dağılmadan kalabiliyorlar. Bu da bize füzyonu, dolayısıyla evrende hidrojenden başlayıp koca periyodik tablonun oluşumuna ışık tutuyor. Yalnızca ışık tutmakla da kalmıyor, kendi yapay (doğada karşımıza çıkmayan) elementleri yaratmanın yolunu açıyor.
Kuantum tünellemenin kullanıldığı benzer bir kuramsal ilerlemenükleer fizyon için de görülebilir, ilgililer “Microscopic Theory of Nuclear Fission: A Review” derleme makalesini inceleyebilirler.
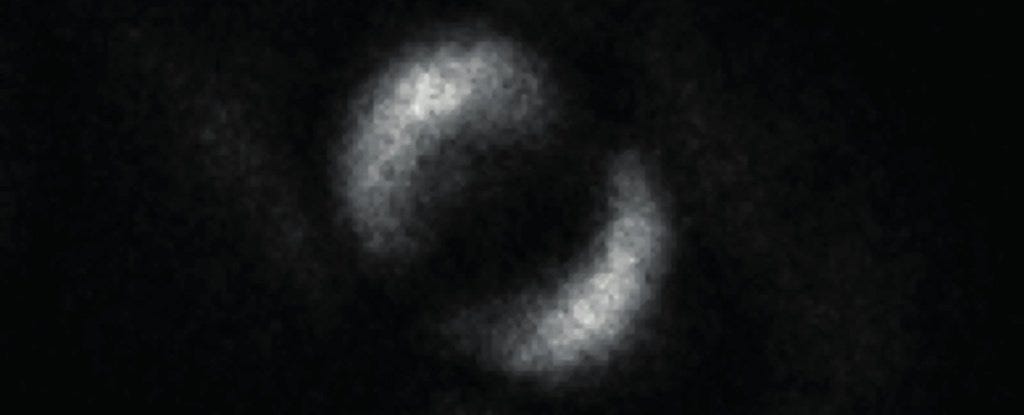
- Dolanıklık: Süperpozisyon durumunun birden fazla parçacığın yerel olmayan korelasyonlara sahip olduğu versiyonu.
Daha önce kuantum dolanıklık üzerine Kutlu’nun “Kuantum Dolanıklık ve Kuantum Işınlama Nedir?” ile benim “Kuantum Dolanıklık ve Güvenli İletişim” ve “Kuantum Bilgisayarların Matematiği Üzerine” yazılarımda değinmiştik. Burada da kısaca özet geçebiliriz.
Elimizde bir bozuk para olduğunu düşünelim. Bu %50 ihtimalle 0(tura) veya 1(yazı) versin. Şimdi bundan iki tane olduğunu düşünelim ve attığımızda hangi ihtimallerin gelebileceğini düşünelim. %25 ihtimalle 00,01,10,11 görebileceğizdir. İstanbul’daki birisinin yerde bulduğu bir bozuk para ile Ankara’daki birisinin cebinde unutup sonra bulduğu bozuk paralar olduklarını düşünelim bunların. Eğer İstanbul’daki para her 0 verdiğinde Ankara’daki de 0, 1 geldiğinde Ankara’daki de 1 geliyor olsaydı ne düşünürdük? Paralar önceden ayarlanmış olmalı değil mi, öbür türlüsü mümkün değil? İşte Einstein da tam olarak böyle düşünüp 1935’te Podolsky ve Rosen’la yazdıkları makalede kuantum dolanıklık fenomenini keşfettiğinde tam olarak bu tepkiyi vermişti. Kesin bunların arkasında bunları birbirine bağlayan daha derin bir oyun var!
Paraların yazı mı tura mı geleceklerini belirleyen parametreler düşünebiliriz, ancak daha bu yazıda üç başlık önce ele aldığımız belirsizlik ilkesini hatırlayın. Eğer attığınız paralar ‘kuantum’ sistemler olsalar da önceden yazı mı tura mı geleceğini tahmin etmek imkansız olurdu. Ama yine de, kuantum mekaniği bu ‘kuantum’ paraların birisi yazı geldiğinde diğerinin de yazı gelmesine, biri tura geldiğinde öbürünün de tura gelmesine matematiksel olarak imkan veriyor. Einstein bu matematiksel gerçeği fark ettiğinde kurulmasına yardımcı olduğu ve Nobel ödülünü o daldan aldığı kuantum fiziğine sırtını döndü, çünkü böylesi bir fenomenin ışık hızından hızlı bilgi aktarımına imkan vereceğini, bunun da saçmalık olduğunu düşündü.
Konu üzerine 1964’te John Bell’in yaptığı formülasyon ve 1982’de Alain Aspect tarafından gerçekleştirilen deneylere kadar dolanıklık hala varlığı üzerine herkesin uzlaşmadığı bir fenomendi. Hala bazıları arkada bir şeylerin döndüğünü ve bunun bir matematiksel oyun olduğunu düşünüyordu. Oysa (Dowling’in de makalede anlattığı üzere) 1994’te British Defence Evaluation and Research Agency tarafından fiber kablolar üzerinden 4-km’de yapılan deneyler kuantum dolanıklığın yalnızca varlığını değil güvenli haberleşme için de kullanılabileceğini deneysel olarak göstermiş oldu. Yine aynı sene Peter Shor’un bilim camiasına tanıttığı Shor algoritması ise kuantum dolanıklığın gücünü kullanabilen bilgisayımsal sistemlerle nasıl günümüz şifreleme sistemlerinin kırılabileceğini gösterdi.
Elbette bu esnada kuramsal çerçevede de pek çok çalışma oldu ve kuantum dolanıklığın, her ne kadar çok işlevli bir fenomen olsa da, ışıktan hızlı bilgi iletişimi için kullanılamayacağı matematiksel olarak gösterildi. Yani Einstein’ın müthiş bir içgörüyle kağıt üstünde keşfettiği bu fenomen onun olabileceğini düşündüğü üzere özel görelilik kanunlarıyla çelişmiyordu (fakat bu Einstein’ın kuantum mekaniğiyle tek derdi değildi, bunu görse bile fikrini muhtemelen değiştirmezdi).
- Eşevresizlik (decoherence): Kuantum sistemlerin zamanla (çevreyle etkileşerek veya yalnızca zamanın geçmesiyle) ‘kuantumluk’larını kaybetmesi ve klasik fizikle açıklanabilir sistemlere dönüşmesi.
Bu, Dowling ve Milburn’ün makalesinde ele alınan altı temel kuantum ilkeden belki de fizikçi olmayanlar için anlaması en zor olanı. Şimdiye kadar hep kuantum sistemlerin sergilediği özelliklerden bahsettik. Ancak bu durumlar stabil değiller. Yani bir kuantum sistemin dengeli bir süperpozisyonda veya dolanık halde durması yalnızca çok kısa süreler için mümkün. Dış faktörlerle etkileşim süperpozisyonu bozup sistemi klasik hale sokabilir, dolanıklığı bozup ‘kuantum’ paralarımızı bildiğimiz paraya çevirebilir.
İşte bu nedenle kuantum teknolojileriyle uğraşırken dış faktörleri en aza indirmek gerekiyor. Elle yapılan bu kuantum durumlar çok iyi izole edilmiş, aşırı soğuk ortamlarda muhafaza edilmeleri gerekiyor. Klasik sistemlerde böyle problemlerle karşılaşmıyoruz, bu nedenle klasik bilgisayarlarımızı küçük çiplere takıp cebimizde gezdirmekte problem çekmezken kuantum bilgisayarları uzay boşluğundan yüzlerce kat daha soğuk ortamlarda tutmak zorunda kalıyoruz.
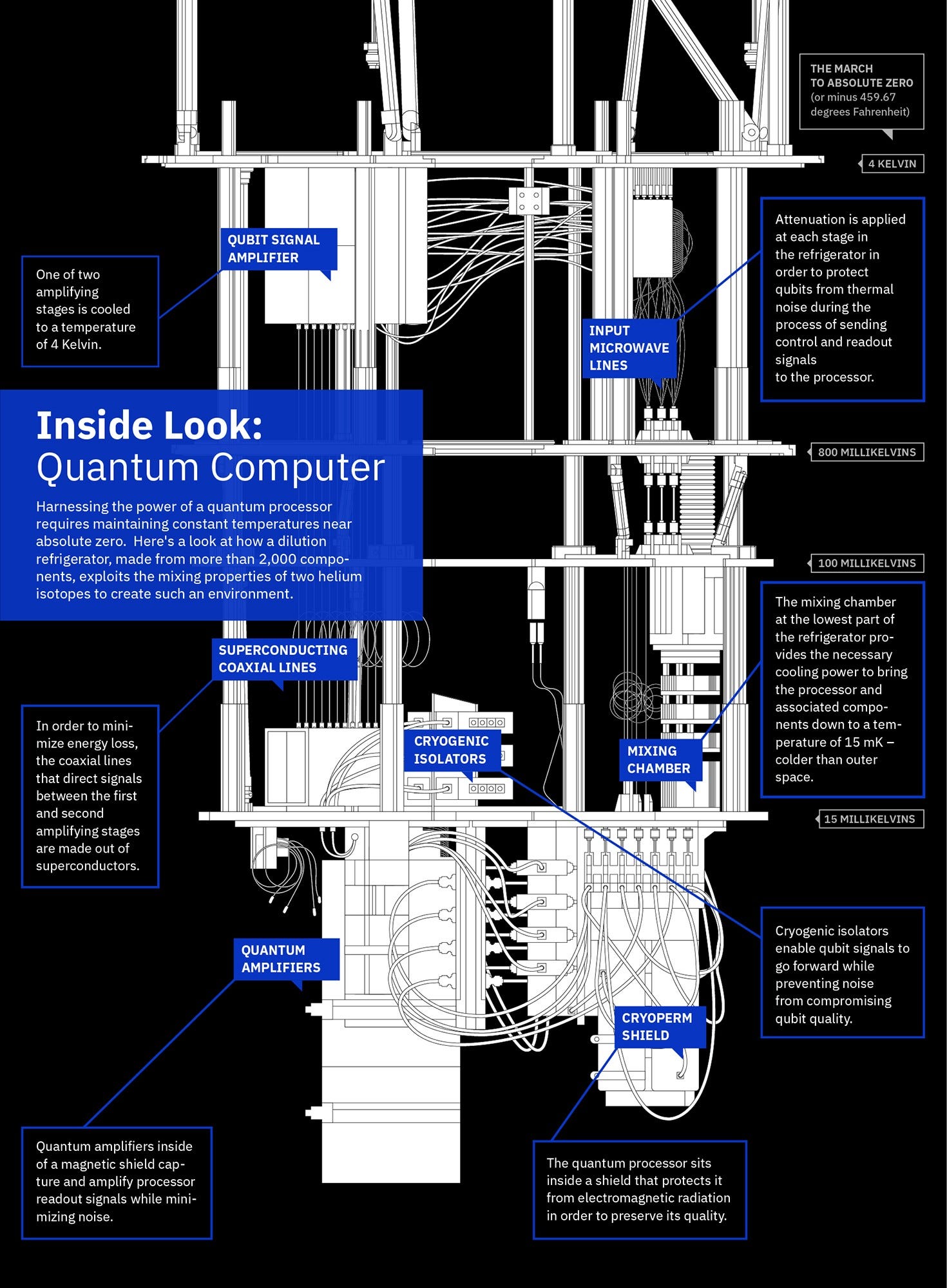
Şimdiye kadar ele aldığımız altı ilke kuantum teknolojisinin üzerine kurulduğu fiziksel prensipleri anlatıyor, makalede bunların sonrasındaysa teknolojilerin kendileri var. Buradaki çoğu teknoloji kendi başına birer yazıyı hak ediyor ama okuyanlar için genel bir çerçeve çizmek adına makalede ele alınan teknolojilerin bazılarını burada sıralayabiliriz: kuantum iletişim protokolleri, kuantum internet, kuantum algoritmalar, kuantum elektromekanik sistemler (QEMS), tek spin sistemlerini kullanan mikroskopi yöntemleri, eşevreli kuantum elektroniği, süperiletken kuantum devreler, spintronik sistemler, atomik lazerler, kuantum optik sistemlerle interferometri, kuantum litografi, etkileşimsiz görüntüleme teknikleri, kuantum ışınlanma, atomik kütleçekim sensörleri…
Sonuç yerine
Dowling bizim için sevilen ve önemli bir figürdü, Twitter ve Facebook alandaki büyük isimlerin kendisinden büyük bir saygı ve sevgiyle bahsettiği anılarla dolu. Kendisinin bize bıraktığı bilimsel pek çok yayının yanında kuantum teknolojisini ve ikinci kuantum devrimini Milburn’le birlikte kavramsallaştırması ileride belki de kitlesel olarak yarattığı en büyük etki olacaktır. Eğer kuantum teknolojileri gerçekten de bugünden öngörüldüğü üzere yeni bir teknolojik paradigmanın kurucu öğeleri arasında yer alacaksa dönüp baktığımızda bu devrimin adını koyan isimlerden biri olarak Dowling’in saygıyla anılacağından emin olabiliriz.










Yoruma kapalı.