Sayısal olarak -1’in karekökü herhangi bir fiziksel niceliğe karşılık gelmez, ancak bu onun fizik biliminde yeri olmadığı anlamına gelmez. Örneğin, bir üsse kompleks bir sayı koymak, üsselin davranışını hızlı büyüme veya bozulma olmadan sabit sinüsoidal salınımlara değiştirir. Burada kastedilen üssel bir fonksiyon hızlıca artar ya da azalırken i konduğunda sabit salınımlı sinsoid bir fonksiyona dönüşmesi. hızlıca artan ya da azalan üssel bir fonksiyonu, sabit sinüsoidal salınımlara dönüştürür. Örnek olarak, bu sayının 62. sayfasındaki Iñigo Liberal ve Nader Engheta’nın çalışmasına bakabilirsiniz)
Elektromanyetizma ve fiziğin diğer birçok alanında, sanal sayılar yalnızca matematiksel bir kolaylıktır. İlgili tüm fenomenler hala reel sayılardan başka bir şey kullanılmadan tanımlanabilir, kuantum mekaniği hariç. Gözlenebilir nicelikler ve olasılıklar reel sayılarla ifade edilir, ancak kuantum durumları ve bunları gösteren denklemler sanal sayılar içerir ve bunları ortadan kaldırmanın basit bir yolu yoktur. Ama bunlar sadece teorik aktarımın bir eseri mi, yoksa gerçekten orada olmaları mı gerekiyor?
Viyana’daki Kuantum Optik ve Kuantum Enformasyon Enstitüsü’nden Miguel Navascués ve meslektaşları, yeni teorik çalışmalarında bu soruya biraz ışık tuttular. Kuantum teorisinin matematiksel olarak nasıl yapılandırılması gerektiğine dair bazı varsayımlara dayanarak, karmaşık değerli formülasyonun tahminlerini hiçbir reel değerli kuantum teorisi formulasyonları ile elde edilemiyor. Ayrıca, gerçek değerli kuantum teorilerini ortadan kaldırabilecek deneysel olarak uygulanabilir bir test tasarladılar. Önerilerinin Ocak 2021’de duyurulmasından bu yana geçen süre içinde, iki grup deneyi gerçekleştirdi ve her ikisi de standart karmaşık değerli kuantum teorisi lehine sonuçlandı.
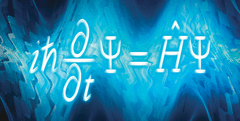
Başka Bir Deyişle
Bir asır önce ortaya çıkışından bu yana, kuantum dünyası klasik sezgilere birçok yönden meydan okudu, hatta önde gelen fizikçiler bile kuantum tuhaflığına karşı çıktılar. Örneğin bir kuantum durumu, kendi üzerindeki her olası ölçümün sonucunu öngörmek için yeterli bilgiyi içermez; bunun yerine, çoğu ölçüm için olası sonuçlar arasında yalnızca bir olasılık dağılımı sunar.
Teorinin öncüleri, şanssız bir şekilde, kuantum dünyasının eksik bir tanımı üzerinde gerçekleşmiş ve aslında her ölçüm sonucunu önceden belirleyen bir yerel gizli değişkenler sistemi tarafından desteklenmeyi beklemiş olabilir mi?
John Bell ve diğerlerinin çalışmaları sayesinde bu fikir çürütüldü. Fark edildi ki kuantum mekaniğinin ve yerel gizli değişkenlerin olası herhangi bir teorisinin farklı sonuçları öngördüğü bir deney tasarlanabilir. Deney, kuantum teorisi cilasının altında tam bir yerel gizli değişkenler kümesinin gizlenemeyeceğini saptamak için yeterlidir. Ancak deney gerçekten yapıldığında, kuantum mekaniğinin her seferinde muzaffer olarak ortaya çıktığı gözlendi
Karmaşık sayıların gerekliliği sorusunun, kuantum teorisinin doğası gereği belirsizliği sorusuyla pek çok ortak noktası vardır, ancak bunun çözümü çok daha zordur. Başka bir adla anılsalar bile, karmaşık sayılarla aynı şekilde davranan yeni matematiksel yapılar her zaman tasarlanabilir. 1960’ların başında, Ernst Stueckelberg kuantum mekaniğinin gerçek değerli formulasyonuyla tam da bunu yaptı. Bu nedenle, sorunun mantıklı olması için, gerçek değerli kuantum teorilerini içermeyen kompleks kuantumu ifade eden bazı temel kurallar oluşturmak gereklidir.
Çok Fazla Boyut
Karmaşık bir sayı olan; a + bi, sıralı bir reel sayı çifti (a, b) ile, yani gerçek sayıların uzayında iki boyutlu bir vektör şeklinde tanımlanabilir. Ancak kuantum durumları karmaşık sayıların çok boyutlu vektörleridir ve boyutların boyutlar üzerinde birleştirilmesi karmaşık hale gelir. Bir spin -1/ kübiti, iki boyutlu karmaşık boyutta bir vektör ile gösterilir. Dört boyutlu reel uzayda bir vektör olarak da yazılabilir, ancak bu boyutlar doğal olarak eşdeğer değildir.
Problem, çok parçacıklı durumların nasıl oluşturulacağı düşünüldüğünde ortaya çıkar. Navascués ve meslektaşlarının, kuantum teorisinin temel bir matematiksel özelliği olarak gördüklerini söyledikleri temel kurallarından biri, iki kuantum sisteminin kombinasyonunun tensör çarpımları ile temsil edilmesidir. (Stueckelberg’in formülasyonu bu kuralı ihlal ediyor.). Örneğin, standart kuantum teorisi, her biri iki karmaşık boyuta sahip iki kübit kombinasyonunun, 8 gerçek boyuta eşdeğer 2 × 2 = 4 karmaşık boyuta sahip olduğunu söyler. Ancak reel değerli bir formülasyonda, aynı iki kübitin her birinin 4 gerçek boyutu vardır ve tensör ürününün 4 × 4 = 16 gerçek boyutu vardır. (sistemi tanımlamak için gereken boyutun iki katı).
Çok fazla boyuta sahip olmak, bir teori için çözülemez bir sorun gibi görünmüyor ancak önceki çalışmalar, iki veya daha fazla dolaşmış parçacığın merkezi bir kaynaktan çıktığı ve uzaysal olarak ayrılmış gözlemciler tarafından ölçüldüğü Bell benzeri deneyleri için, tensör-çarpım kuralının kısıtlamasıyla standart kuantum mekaniğinin tüm tahminlerini taklit eden gerçek değerli teorilerin formüle edilebileceğini göstermiştir.
Peki ya boyutların sayısı artmak yerine azaldığında? Aşağıdaki şekilde çizildiği gibi, bir dolaşıklık değiştirme deneyi de konu alınabilir. Tek bir kaynaktan oluşturulmak yerine, ayrı kaynaklar tarafından iki grup dolaşık kübit oluşturulur. Gözlemci olan Bob, her bir çiftten (B1 ve B2) bir kübit alır ve diğer ikisi, A ve C, sırasıyla Alice ve Charlie’ye gider.
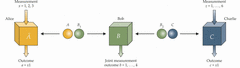
Bob daha sonra iki kübiti üzerinde ölçüm yapar, dört olası sonuç vardır. Karmaşık değerli kuantum mekaniğinde, bu ölçüm sistemin boyut sayısını yarıya indirir ve dolanık çiftlerin sayısını ikiden bire indirir. Yani, dolaşıklığı A ve C kübitlerine aktarır. Ancak gerçek değerli bir formülasyonda, Bob’un dört-sonuçlu ölçümü, dolaşıklığı tamamen değiştirmek için boyutluluğu yeterince düşürmez; bunu yapmak için 8-sonuçlu- ölçüm yapması gerekirdi ve böylece A ve C kübitleri tamamen dolaşık hale gelmez.
Boyut uyuşmazlığı, özellikle ekstra boyutların ilk etapta orada olması gerekmiyorsa, gerçek değerli teorinin sistemi tanımlayamayacağı anlamına gelmez. Navascués ve meslektaşları, bunun mümkün olmadığını kanıtlayana kadar, gerçek değeri olan açıklamanın işe yaraması için çok zaman harcamışlardı.
Reel Kompleks
İmkansızlığın matematiksel kanıtları, mümkün olanın inşasından çok daha zor olabilir. Kuantum mekaniğinin (tensör-çarpım kuralı) karmaşık sayılara ihtiyaç duyduğunu göstermek için Navascués ve meslektaşları, yalnızca reel değerli formülasyonun işe yaramadığını değil, hiçbirinin işe yaramadığını kanıtlamak zorunda kaldılar. Belki de her karmaşık boyutu iki gerçek boyutla temsil etmek en doğal olanıdır, ancak gerçek değerli teorilerin bu kadar sınırlı olması gerekmez. Karmaşık boyut başına üç reel boyut olabilir veya dört, hatta belki de sonsuz sayıda.
Tüm olasılıkları hesaba katmak göz korkutucudur. Yardım, Antonio Acín(aynı zamanda yeni makalenin ortak yazarlarından biri) ve meslektaşları tarafından kuantum bilgi ağları için dolaşıklığın onaylanmasıyla ilgili yakın tarihli bir makale ile geldi. Navascués ve meslektaşları, bu çalışmayı baz alarak, dolaşıklık değişimi deneyi için bir ölçüm korelasyonu fonksiyonunun, standart kuantum teorisinde 6√2=8.49’a ulaşabildiğini buldular. Ancak bu değer gerçek değerli bir formülasyonda 7.66’yı geçemiyor.
Bu çok fazla hareket alanı değil ancak Navascués, gerçek değerli sınırın önemli ölçüde iyileştirilebileceğinden şüpheleniyor. Araştırmacılar sayısal olarak hesaplamaya ilk çalıştıklarında bilgisayarlarının belleği yetmedi. Sonunda, onlara umduklarından çok daha gevşek bir sınır veren bazı yaklaşımlar yapmak zorunda kaldılar.
Yine de, Hefei’deki Çin Bilim ve Teknoloji Üniversitesi’ndeki Jian-Wei Pan ve meslektaşları, süper iletken kübitler kullanarak deneyi yaptıklarında, karmaşık kuantum teorisi alanında rahatlıkla 8.09 değerini gözlemlediler. Jingyun Fan (Shenzhen, Çin’deki Güney Bilim ve Teknoloji Üniversitesi’nden) ve meslektaşları fotonları ilgili bir miktarı ölçmek için kullandıklarında, karmaşık değerli kuantum mekaniğini mantıklı buldular.
Bell testleri gibi, bu deneyler de bazı ince ayarlamalara tabiidir. Ölçümler, gözlemciler arasında sonuçlarını etkileyebilecek herhangi bir klasik bilginin geçmesini önlemek için eş zamanlıya yeterince yakın olmalıdır. Ayrıca korelasyon eşiğinin sadece tespit edilen denemeler tarafından değil, hepsi tarafından karşılanmasını sağlamak için yeterli sayıda ölçüm yapılmalıdır. Bu saydıklarımız gerçekleşmezse, kuantum benzeri korelasyonların sadece gerçek değerli bir teori tarafından değil, klasik bir teori tarafından da taklit edilmesi mümkündür. Bell testlerindeki boşlukları kapatmak; yalnızca 2015’te meyvelerini veren ve on yıllarca süren bir çaba örneğiydi.
Ne Pan’ın ne de Fan’ın grubu, deneylerindeki boşlukları henüz kapatmadı. Bu nedenle teknik olarak, gerçek veya karmaşık sayıların kuantum dünyasının daha iyi tanımlayıcıları olup olmadığı konusunda jüri hala kararsız. Yine de, kuantum mekaniğinin gelecekteki öğrencilerinin, sayıların matematiğiyle boğuşmaya devam etmekten başka seçenekleri olmayacak gibi görünüyor.
Yazar: Abdüsselam Yüceer
Redaktör: Berfu Deniz Kara









Yoruma kapalı.