
Bu yazı kuantum fiziğini merak eden ama oturup fizikçiler için yazılmış bir ders kitabını okumaktan gözü korkan (veya üşenen) kişilere yöneliktir. Yazının akışı içerisinde yapılan tanımlarla aslında kuantum fiziği öğrenmek için öncül neleri bilmeniz gerektiğine de adım adım vurgu yapılmıştır. Yazının sonunda hepsini bir liste halinde bulabilirsiniz.
Fizik Nedir?
Daha önce “Fizik Nedir, Fizikçi Ne Yapar?” başlıklı yazımızda değinildiği üzere (indirgemeci yaklaşacak olursak) Fizik bilimi aşağıdaki şekilde özetlenebilir:
…fiziksel bir sistemin matematiksel tasvirini çıkarmak, sonrasında bu matematiksel tasvir üzerinde fiziksel dünyada karşılığı olduğunu varsaydığımız operasyonları uygulamak, sonucunda çıkan matematiksel tasvirin fiziksel gerçekliğini test etmek aşağı yukarı fiziğin tüm öngörü yetisinin metodunu teşkil eder.
Peki buradaki matematiksel tasvirle fiziksel gerçeklik arasındaki bağlantıdan kasıt nedir, kısa bir örnekle başlayalım.
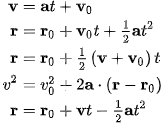
Yukarıda gördüğünüz denklemlere basitçe ‘hareket denklemleri’ denir, üniversiteye geçiş sınavında fen sorusu çözmüş herkes görmüştür. Burada r bir cismin kafamıza göre belirlediğimiz bir merkeze olan uzaklığı, v yine aynı uzaklığın değişimini (yani cismin hızını), a ise değişimin değişimini (yani cismin ivmesini) verir. Bu denkleme göre sabit ivmeli bir cismin r, v ve a’sını biliyorsanız herhangi bir zamanda ne yapacağını bilebilirsiniz! O zaman neden her şeyin nasıl hareket edeceğini bilemiyoruz? Çünkü çoğu şey sabit ivmeli hareket yapmaz, ivmesi de zaman göre değişir. Yani yukarıdaki denklemler ‘özel koşullar’ altında doğru denklemlerdir (bu özel koşullar meselesi yine karşımıza çıkacak).
Şimdi farklı bir ‘matematiksel tasvir’ anlatımına geçelim, istatistiksel bir anlatım. Yani hadiseleri kesin olarak oldu veya olmadı diye tanımlamaktansa p ihtimalle oldu ve 1-p ihtimalle olmadı diye tanımlayabiliriz. Burada toplamın 1 olması tüm olasılık uzayını tasvire dahil etmek için önemlidir. Örneğin birisi size iki seçenek sunarsa, birisi %30 birisi %50 ihtimalle doğru derse, aslında ortada %20 ihtimalle başka bir seçeneğin olması gerektiğini de bilirsiniz. Bu durum olasılık toplamının %100, yani basitleştirilmiş haliyle 1 olması gerektiğinden kaynaklanır. Elinizdeki seçeneklerin olasılıkları da 0.3 ve 0.5 olarak yazılır.
Bu anlatım içerisinden devam ederek, diyelim ki oturduğunuz yerde havaya bir top attınız. Top yüksek ihtimalle sizin oturduğunuz yere geri düşecek. Ama sonuçta dünyanın binbir türlü hali var, belki biraz yamuk attınız belki o esnada rüzgar esti. Bunların hiçbirini bilmediğinizi göz önüne alırsak topun nereye düşeceğinin olasılıklarını ‘normal’ dağılıma göre hesap etmeniz en rasyonel hareket olurdu. Yani havaya attığınız top yüksek ihtimalle sizin olduğunuz yere, biraz daha düşük ihtimalle yakın çevrenize, düşük ihtimalle biraz uzağınıza, sıfır ihtimalle yan odaya düşecektir. Aşağıda bunun görselleştirilmiş halini bulabilirsiniz.
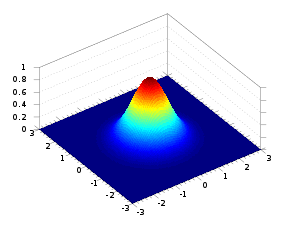
Neden resminin daha çekici olduğunu anlamak için denklemine de bakabiliriz.
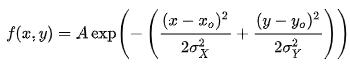
Burada x ve y değişkenlerimiz, yani topun nereye düşme ihtimaline bakmak istediğimiz. Tam olduğumuz yere x_0 ve y_0 diyoruz (yukarıdaki resim için bu 0,0 noktası ama istediğinizi diyebilirsiniz). Üstteki x-x_0’ın aşağısındaki o garip üstü çizikli O (sigma)_X, diğeriyse sigma_Y, bunlar da topu ne kadar düzgün atmadığınıza yönelik sapma oranları (standart sapmalar).
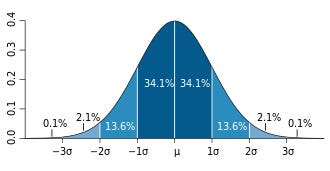
Aynı anda iki boyuta bakmak yerine problemi tek boyuta (mesela top ne kadar önünüze veya arkanıza düşecek) indirgediğimizde de yukarıdaki görüntü karşımıza çıkar. Denklem yine aynı, yalnızca y ile ilgili kısmı kaldırıp atın.
Peki ya topu mükemmel atmışsanız ne olacak, sigma_X sıfır olacak. Bu da denklemdeki herhangi bir değer için e üzeri eksi sonsuz, yani 1 bölü e üzeri sonsuz, yani 1 bölü sonsuz, yani sıfır demek — tek bir yer hariç, tam olarak olduğunuz nokta, yani denklemin e üzeri eksi sıfır bölü sıfır olup matematiksel olarak patladığı yer (matematiksel tekillik teknik terimi, ama patlamak da diyebiliriz). E topun bir yere düşmesi gerekiyor, ama denklem bize açıkça tam olduğumuz yer hariç her yerin sıfır olasılık verdiğini söylüyor, o zaman biz de ne diyoruz, topun bizim olduğumuz yere düşme ihtimali %100 yani 1! Tasviriyse aşağıdaki resim.
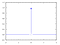
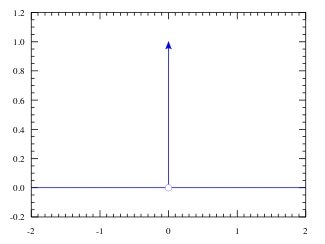
Yukarıdaki top atıp düşürme hikayesinden ne öğrendik? Fiziksel bir problemi (havaya top attık) önce cevaplanabilir bir soruya indirgeyip (top nereye düşecek) sonra da bunun matematiksel tasvirini yaptık. Bahsettiğimiz hareket denklemlerinin aksine yukarıdaki hikayenin hiçbir yerinde hız ve ivme geçmiyordu, çünkü yukarıdaki problemde tek ilgilendiğimiz şey topun nereye hangi olasılıkla düşeceğiydi. Peki topun kütlesi değişse ne olurdu veya atış hızımız ya da ivmesi? Bunların hepsi yukarıdaki denklemde yalnızca standart sapmayı (sigma_X) etkileyecekti. Tanımladığımız problemin ‘koşulları’ altında (durduğunuz yerden tam yukarı doğru top atıyorsunuz) yukarıdaki denklem size ‘bu top nereye düşecek’ sorusunun yanıtını vermek için yeterli.
Bu kısımdan bilmemiz gereken şeyler, bir fiziksel özellik bazı parametrelere bağlı bir fonksiyon olarak nasıl gösterilir ve olasılık dağılımı bir fonksiyon olarak nasıl tasvir edilir.
Kuantum Fiziği Nedir?
Buradan kuantum fiziğine geçişi biraz hızlı yapacağız, ama her kuantum fiziği kitabında anlatılan ‘morötesi felaket (ultraviolet catastrophe)’ meselesine yine de değinelim. Işığın dalga boyu küçüldükçe frekansı yükselir, yani daha yüksek enerjili hale gelir. Herhangi bir objeyi ısıttığınızda ise ışık saçar. Klasik fiziğin denklemleri bize bu saçılımın yoğunluğunun aşağıdaki resimde Rayleigh-Jeans yasası olarak tanımlanan şekilde olacağını söyler.
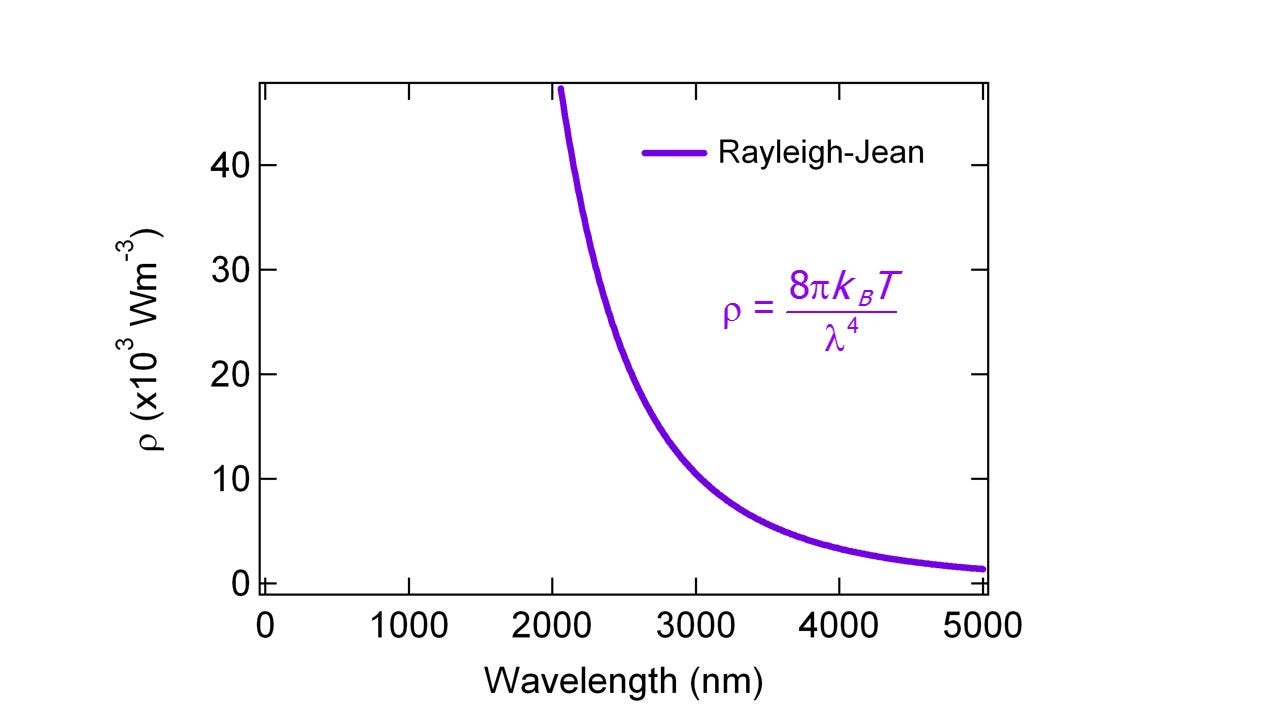
Ki bu ciddi bir yanlış ve sorundur. Bu yasaya göre ısınmış bir obje neredeyse sonsuz yoğunlukta çok yüksek enerjili ışık saçacaktır! Gerçek dağılımsa aşağıdaki gibidir.
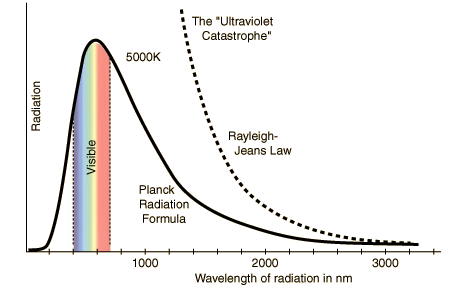
Sanırım ‘Planck’ radyasyon formülünü görmek bir şeye işaret etti. Planck’ın kurguladığı haliyle bu formül ‘Planck’ sabiti denilen bir şeyi denkleme ekler, bu da fiziksel olarak ısınmış objelerin radyasyonu (yani enerjiyi) sürekli değil de kesikli şekilde (enerji paketçikleri) cinsinden saçtığı varsayımına dayanır. Denklem bu varsayımla başlayınca yukarıdaki Rayleigh-Jeans’ten aşağıdaki hale dönüşür.
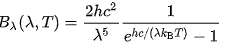
Planck bu varsayımı sırf yukarıdaki resimdeki çizgiyi sağlayacak fonksiyonu elde etmek için koyar. Enerji saçılımının sürekli olmasıyla derdi olan bir insan değildir, hatta varsaydığı kesikli enerji saçılımıyla birinci kuantum devriminin ateşini yakacağını da bilmemektedir. Derdi fizik yapmaktır, yani elindeki deneysel resme uyan matematiksel tasviri (fonksiyonu) bulabilmek. Kuantum mekaniğini başlatan bir diğer teori-deney uyuşmazlığı içinse fotoelektrik etki olayına bakabilirsiniz, o hikayenin kahramanıysa Einstein’dır.
Planck ve Einstein’ın 1900’lerin ilk 5 senesinde keşfettiği bu gerçekler araya Birinci Dünya Savaşının girmesine rağmen dünyanın çeşitli yerlerindeki fizikçiler tarafından yoğunlukla çalışıldılar. Bundan yirmi sene sonra, 1925’e geldiğimizdeyse elimizde neredeyse tamamlanmış bir teori vardı, kuantum mekaniği!
Mekanik Nedir?
Öncelikle düz bir şekilde mekanik nedir diye soracak olursak: Mekanik, kuvvetlerin etkisi altındaki cisimlerin hareketli ve durağan hâllerini inceleyen bilim dalıdır (Vikipedi).
Mechanics, science concerned with the motion of bodies under the action of forces, including the special case in which a body remains at rest. (Brittanica)
Yukarıdaki hikayede Planck ve Einstein’ın keşiflerini düşünün, küçük enerji paketçikleri, ışık tanecikleri, teker teker elektronlar… yani aklımızın asla gündelik tecrübelerimizle kavrayamayacağı fiziksel öğeler (bu meseleye dair “Sistemler ve Boyutları Üzerine” yazımı da tavsiye ederim). Kuantum mekaniği ise bu cisimlerin hareketli ve durağan hâllerini inceleyen bilim dalı diyebiliriz. Yani elimizde çok küçük nesneler var, bunlar çeşitli fiziksel kuvvetlere maruz kalıyorlar, halleri nicedir diye sorup bunu yanıtlamaya çalışmak. Bu cisimlerin fiziksel özelliklerinin de yalnızca ‘kesikli’ haller alabileceğini keşfettiğimiz için buna kuantum mekaniği diyoruz, kuantum fiziğindeki ‘kanunlara’ göre inceliyoruz hareketi (veya durağanlığı).
Burada hazır ‘hal’ lafı geçmişken hikayeye ‘kuantum hal (quantum state)’ nedir diye başlayalım. Yukarıda gördüğünüz kocaman Yunan harfi Psi. Genelde bir cismin kuantum halini tasvir ederken bu harfi kullanıyoruz. Psi(x) bir cismin pozisyonunu tasvir eden kuantum hali, yani pozisyona bağlı bir fonksiyon. Psi(p) ise örneğin bir cismin momentumunu tasvir eden kuantum hali. Psi(xox) desek bu da o cismin xox hangi fiziksel nicelikse ona bağlı fonksiyonunu tasvir eden kuantum hali olurdu. Peki bu Psi fonksiyonu neyi tasvir ediyor? İşte bu, kuantum mekaniğini anlamak isteyenler için en önemli nokta.
Yukarıdaki top örneğinde verdiğimiz f(x,y) fonksiyonunu ele alalım. Oradaki f(x,y)=z fonksiyonunda z değeri bize o topun x,y koordinatlarına düşme ihtimalini veriyordu. Yani f fonksiyonuna herhangi x ve y parametrelerini girip “havaya düz atılan topun x,y koordinatına tekabül eden yere düşme ihtimali”ni elde edebiliyordunuz. Mesela 1 metre ilerinize ve 1 metre sağınıza düşme ihtimalini f(1,1) veriyordu (x ve y’yi metre cinsinden tanımladıysanız, atıyorum cm cinsinden tanımladıysanız f(100,100) aynı değeri verir).
Bu f fonksiyonunun değeri 0 ila 1 arasında değişiyor ve tüm olası x ve y’ler için değerlerini topladığınızda size tam olarak 1 veriyor, çünkü tanımı böyle. O top mutlaka bir yere düşecek, dolayısıyla topun HER YERE düşme olasılığının toplamı 1 olmak zorunda. Tekrar aşağıdaki dağılımı hatırlayalım.

Yukarıdaki resimde tüm mavi yerleri ‘toplarsanız’ size toplam vermesini istediğiniz sayı tam olarak 1 olacak. Yukarıdaki toplam yapmak (yani bir çizginin altında kalan alanı belirlemek) için elimizdeki matematiksel aletse integral (evet integral almak bu işe yarıyor — buraya kadar okuduysanız lütfen integral kelimesini görüp kaçmayın, iyi gidiyorsunuz).
O zaman f(x,y) yerine Psi(x,y) yazarsak mesela bir elektronu da havaya atınca düşeceği yeri bulamaz mıyız? İşte tam olarak bu soru kuantum hal dediğimiz fonksiyonun klasik olasılık dağılımı fonksiyonundan farkını veriyor. Psi(x,y) aslında f(x,y)’ın karekökü — sayılır.
Klasik fizikte örneğin havaya iki top attınız, bu topların ikisi de f(x,y)’a göre davranacaklar, hatta topları teker teker attığınız bir senaryoda bir top atmanızla sonsuz top atmanız arasında hiçbir fark yok. Oysa kuantumda bu işlerin böyle olmadığını biliyoruz. Bunun en ünlü örneğiyse çift yarık deneyi (bu konu üzerine Kutlu Kutluer tarafından yazılmış olan yazıyı ilgililere tavsiye ederiz — Kuantum Süperpozisyon ve Çift Yarık Deneyi Nedir?).

Elektronları teker teker attığınızda ve ortada bir delik varsa yukarıda solda gördüğünüz gibi davranıyorlar, yani bir ‘normal’ dağılım fonksiyonu görüyorsunuz, bildiğimiz havaya top attım nereye düşecek cinsinden bir f(x) dağılımı. Peki ortada iki delik varsa ve elektronları teker teker atıyorsak ne görmeyi bekleriz, sağda yukarıdaki gibi iki normal dağılımın üst üste binmesini. Bunun yerine elektronları ‘teker teker’ atsanız bile sağ alttaki dağılımı görüyoruz. Kuantum fiziğinde dalga-parçacık ikiliği diye de geçen bir konudur bu. Parçacıklar (mesela havaya attığımız top) soldaki ve sağ üstteki gibi davranıyorlar. Dalgalar ise yapıcı ve yıkıcı girişim yapabiliyorlar, yani sağ alttaki gibi davranıyorlar. Elektronları teker teker attığınızda tek bir delik varsa parçacık gibi davranıyorlar, ama iki delik varsa girişim yaparak dalga gibi davranıyorlar. Bu paragrafta ‘teker teker’e olan vurgu elektronlar birbirlerini etkilemiyor olsalar bile koşuluna vurgu yapmaktı, arkadan gelen itiyordur gibi argümanlar bundan onlarca sene önce deneysel olarak yanlışlandı, tek bir tane elektron atsanız bile böyle davranıyor diyebiliyoruz.
O zaman bir sistemin kuantum halini anlatan fonksiyon bildiğimiz anlamda basit bir olasılık dağılımı fonksiyonu olamaz, ki zaten de değil. Psi(x) bildiğimiz olasılık dağılımı olan f(x)’in karekökü. Ama öyle düz karekökü de değil, kompleks uzayda karekökü! Ama önce bildiğimiz fonksiyonların kareköküyle başlayalım.
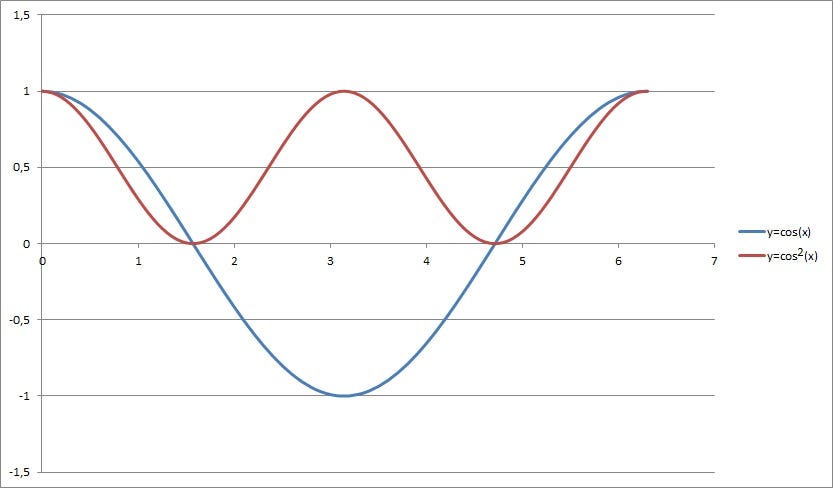
Yukarıda gördüğünüz x’e bağlı bir kosinüs fonksiyonuyla karesinin aynı resimde gösterilmesi. Kosinüs fonksiyonu gördüğünüz üzere eksi değerler alabiliyor, ancak karesini aldığınızda hep pozitif değerler veriyor. Yani eğer biz f(x) gibi, 0 ila 1 arasında değerler alabilen bir fonksiyon istiyorsak kosinüs fonksiyonunun karesini, yani f(x) = Acos²(x) gibi bir fonksiyon kullanabiliriz. Ama dalga özelliği gösterip girişim yapan bir şey istiyorsak Psi(x) = Bcos(x) gibi bir şey kullanmamız gerekiyor. Yani öyle bir fonksiyon olmalı ki karesini alınca bize hep 0 ila 1 arasında değerleri olan bir şeyler versin. Ama biz bunun girişim de yapabilmesini istiyoruz.
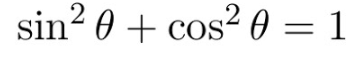
Bu resimdeki yeşil çizgi kosinüs, kırmızı çizgiyse sinüs fonksiyonu. Liseden belki bazılarınız hatırlar, bu iki fonksiyonun karelerinin toplamı hep 1 verir. Biz karelerinin toplamı hep 1 verecek bir fonksiyon istemiyoruz, ama bu fonksiyonun üzerinde biraz oynarsak istediğimizi elde edebileceğiz gibi duruyor. Zaten bu tam da Schrödinger’in yaptığı şey ve kuantum haline bir ‘dalga fonksiyonu’ denmesinin sebebi de buradan, çünkü kosinüs ve sinüs fonksiyonları bizim dalgaları tasvir etmek için kullandığımız fonksiyonlar!
İşte burada işin içine kompleks uzay giriyor. Kompleks sayılar aslında bildiğimiz sayılarla çalışırken üzerinde küçük oyunlar yapmak için icat ettiğimiz ama sonrasında her yerde karşımıza çıkmaya başlayıp “acaba bunlar bizim kolaylık olsun diye uydurmamızdan daha derin anlamları olan şeyler mi” sorusunu sordurup koskoca matematik felsefesi alanları açmış bir matematiksel numara. Örneğin x,y koodinatınız var ama ikisiyle bir sebepten ötürü birlikte çalışmak zorundasınız, o zaman z = x + iy diyebilirsiniz, z burada kompleks bir sayıdır ve aslında z(x,y) gibi bir fonksiyondur da. Ancak şu an burada detayına girmeyeceğimiz pek çok ‘özel koşul’u olan bir fonksiyon.
Resimde gördüğünüz üzere e^(ix) = cos(x) + i sin(x) kompleks uzayda merkezden 1 birim uzaklıktaki bir çemberi işaret eder. Peki bu çemberin tamamının boyunu ölçersek ne buluruz, 2π (hatırlayın 2 pi r diyorduk, eğer r 1 ise çevre 2 pi olur)! E o zaman bu fonksiyonu 2π’ye bölersek bu fonksiyonun tüm uzaydaki toplam değeri kaç olur, 1, aha tam da aradığımız şey! Fakat unutmayın bizim istediğimiz şey kompleks değil reel uzayda 1 elde etmek, hatta özel olarak 0 ila 1 arasında değeri olan bir reel sayı elde etmek.
Şimdi burada kompleks sayıları bilmeyenleriniz için anlamsız gelecek olsa da kompleks uzaydan pozitif reel sayılara geçerken kullandığımız küçük bir numara var. Kompleks sayı i’nin karesi, yani i kere i tanım itibariyle -1 ediyor (karmaşık sayılar üzerine). O nedenle pozitif sayı vermesini isteyerek karesini alıyorsak i’nin karesini i kere -i diye tanımlıyoruz, böylece i’nin karesi 1 veriyor. Aşağıdaki hesabı takip ederseniz neden böyle bir numara yaptığımızı anlayacaksınız.
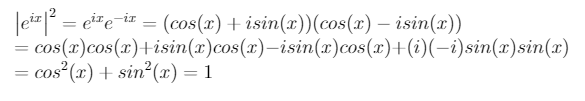
Yani eğer Psi(x) = e^(ix) sizin kuantum halinizin fonksiyonuysa f(x) = |e^(ix)|² da sizin olasılık dağılımınız olacak. E ama bu f(x) tüm x değerleri için 1 veriyor ama biz bir çember üzerinde herhangi bir yerde olabiliriz aynı anda 100% ihtimalle her yerde olamayız? İşte o nedenle f(x) fonksiyonumuzu 2π’ye bölmemiz gerekiyor, bu da e^(ix) fonksiyonunu karekök 2π’ye bölmemiz demek. Daha da uzatmadan aşağıdakileri elde ettiğimizi diyebiliriz.
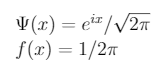
Kutlarım, ilk kuantum dalga fonksiyonunuzu başarıyla tamamladınız (kısmen)! Şimdi kendinize küçük bir ödül verip bu yazıya devam edebilirsiniz.
Kuantum Hal — Fiziksel Anlam
Buraya kadar derdimiz bir kuantum durum yazabilmekti, şimdiyse verilmiş bir kuantum durumu okumayı öğrenelim. Örneğin Psi(x) = e^(ix) / karekök içinde 2π, bu durum bize fiziksel olarak neyi tasvir ediyor?
Yukarıdaki çemberden hatırlayın, buradaki x değerimiz ne değerini alırsa alsın hep çemberin üstünde bir yere tekabül ediyor. Dolayısıyla örneğin şöyle bir sistemi tasvir ediyor olabilir, biz ortada duruyoruz ve bir yöne dönüp o tarafa doğru bakıyoruz. Nereye döndüğümüz de x parametresi. E aynı yöne bir sürü farklı x denk geleceğinden de diyebiliriz ki “yalnızca çember üstündeki ilk turumuzu hesaba katacağız, sonrası bu ilk turdakinin tekrarı olacak zaten”. Bunlara matematiksel olarak periyodik fonksiyonlar denir, aynı hareketi belirli bir periyotla tekrarlayan davranışları tasvir etmek için biçilmiş kaftan.
O zaman x = 0 tam ileri, x = 90 sağa, x = 180 arkaya, x = 270 sola bakmak diyelim. Bu durumda x’in periyodu 360 olur. Yani Psi(0)=Psi(360)=Psi(720)=….. diye gider, aynı şekilde Psi(90)=Psi(450)=… olduğunu da görmek kolay. Bir çemberin 360 derece olduğunu bildiğimiz için böyle dediğimiz elbette aşikar, eğer uygun matematiksel oynamaları yaparsak x =0,1,2,3 de diyebiliriz, keyfimize kalmış.
Birisi sizi tutup kendi çevrenizde döndürse ve siz “durduğumda hangi yöne bakıyor olurum acaba” diye merak etseniz elde edeceğiniz fonksiyon f(x) = 1 / 2π olurdu, her yöne bakma ihtimaliniz eşit! Bunun kuantum hali de yukarıdaki Psi(x) olurdu. Dolayısıyla önünüzle sağınız arasında bir yere bakıyor olma ihtimalinizi hesaplamak isterseniz bunu |Psi(x)|²‘nin 0’dan 90’a kadar integralini alarak yapıp bulabilirdiniz! Şimdi diyebilirsiniz ki “e ben bunu direk f(x)’in 0’dan 90’a kadar integralini alarak da yapabilirim”, haklısınız, ama unutmayın siz bir kuantum parçacığı değilsiniz! Sadece f(x) = 1 / 2π sizin sorunuzu çözmeye yeter. Asıl kuantum fiziğine gerek duyacağınız (ve giriş yapacağımız) yer bundan sonra başlıyor.
Psi(x) = e^(ix) / karekök içinde 2π — bu aslında (bazı katsayıları atılmış olarak) serbest uzayda, hiçbir kuvvetin etkisi altında olmayan bir parçacığı nerede bulacağınızı kestirmek için yazdığımız bir kuantum hal. Unutmayın kuantum parçacıklar dalga gibi de davranabiliyor diye bunları tasvir etmek için dalga denklemlerini kullandık. Ama parçacığı ölçtüğümüzde tüm dalgaya yayılmış olarak değil tek bir yerde buluyoruz. Psi(x) aslında ölçüm sonucunda parçacığı nerede bulacağımızı veren olasılık dağılımının karekökü, yani teknik terimle olasılık genliğimiz.
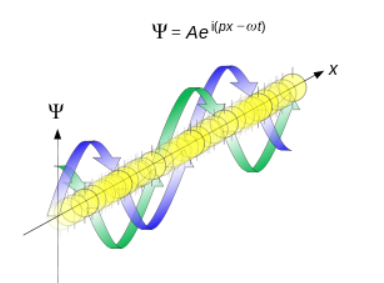
Psi denklemenin bizim yazdığımız e^(ix)’li halinden biraz farklı olduğunu yukarıda görebilirsiniz. Oradaki p parçacığın momentumunu (kütleli parçacıklar için bu bildiğimiz p=mv denklemi gibi düşünebilirsiniz), w frekansını, t ise geçen süreyi temsil ediyor. Ama buradan f(x)’e geçiş yapıp olasılık dağılımına bakacak olursanız bunun her x değeri için f(x)=|A|² verdiğini görebiliriz. Yani serbest uzayda, hiçbir kuvvetin etkisi altında olmayan bir parçacık her yerde olabilir!
Şimdi bir dur deyip düşünebiliriz. Elimde bir parçacık var, x=0 lokasyonunda (elimde) duruyor, zaman da hiç geçmedi, bu parçacık nasıl her yerde olabilir İşte burada kuantum fiziğinin bir diğer özelliğini devreye sokmamız gerekiyor, belirsizlik ilkesi.
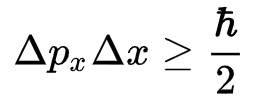
Heisenberg’in belirsizlik ilkesi Schrödinger ile eşzamanlı olarak kuantum mekaniğini farklı bir şekilde kurmuş olan Werner Heisenberg’in matematiksel olarak gösterdiği temel bir ilkedir. Basitçe ifadesi şöyledir, bir parçacığın momentum ölçümleri sonucundaki standart sapma ile pozisyon ölçümleri sonucundaki standart sapma mutlaka Planck sabitinin yarısından büyük olmak zorundadır. Buradaki standart sapma istatistiksel standart sapmadan biraz farklı hesaplanır ama sonuç olarak çok benzer bir işleve sahiptir.
Eğer “Elimde bir parçacık var, x=0 lokasyonunda” derseniz x’in standart sapması sıfır demektir, bu da momentumun standart sapmasını sonsuz olmak zorunda bırakır. Parçacık kesin olarak elinizdeyse hızı sonsuzla sıfır arasında herhangi bir şey olabilir. Bu da bizi dalga-parçacık ikiliği resmine ve aşağıdaki eşitliğe geri götürür.

De Broglie dalgaboyu Louis de Broglie tarafından gösterilen ve p momentumuna sahip bir parçacığın ‘dalga boyu’nu veren eşitliktir. Bir parçacık ne kadar küçükse dalga boyu o kadar yüksektir. Dolayısıyla büyük nesnelerin dalga boyu çok küçüktür (akıl alamayacak kadar küçük), oysa çok küçük nesnelerin büyüktür. Yani De Broglie dalga boyu bize dalga-parçacık ikiliğinde tasvirler arası geçiş yapma imkanı sunar. Şimdi elinizdeki parçacığın pozisyonundaki standart sapma sıfırsa momentumu herhangi bir şey olabilir. Diyelim momentumu çok küçük, o zaman dalga boyu çok yüksek olur. O zaman da sizin ‘elinizde’ olduğunu iddia ettiğiniz parçacık aslında çok geniş alana yayılmış bulunmaktadır, şu an elinizde olması aynı parçacığın aynı koşullar altında ‘yine’ elinizde olacağını söylemez.
Bu nedenle de ‘elinizdeki’ parçacığın tek ölçüm sonucunda x=0’da aslında orada olduğunu göstermez. Kuantum mekaniği olasılıksaldır, dolayısıyla ölçümleriniz istatistiksel olmalıdır. Elinizdeki parçacığınız yerini 1000 kere ölçtüğünüzde bazı ölçümleriniz x=-1, bazıları x=+1 gibi şeyler de gelebilir. “Parçacık benim elimde” demek x=0’ın bunların hepsinin ortalamasında elinizde kalan değer olmasına denir. Çünkü parçacığı x=0’da görmüş olmanızla x’in standart sapmasının sıfır olması denk durumlar değildir.
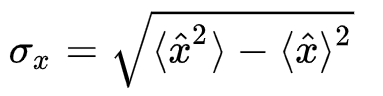
Standart sapma kuantum fiziği için yukarıdaki gibi hesaplanıyor. Yani sizin elinizde x=0 olması standart sapmanız sıfır değilse x²=0 olmasını garanti etmez! Bu durumda standart sapmanızı ne kadar genişletirseniz parçacığın momentumuna dair o kadar gerçekçi konuşabilmeye başlarsınız.

Ancak bir detaya daha dönelim, biz Psi(x) denkleminden bahsediyoruz, yani p — momentum bizim için bir değişken değil. Neden Psi(x,p)’den bahsetmiyoruz? Uzatmamak adına burayı kısa geçerek diyebiliriz ki Heisenberg belirsizlik ilkesi ve bu ilkenin dayandığı sırabağımlılık (non-commutativity) bizim fiziksel olarak tutarlı sonuçlar veren bir Psi(x,p) denklemi yazmamızı engelliyor. Dolayısıyla ya Psi(x) ya Psi(p) yazabiliyoruz, Psi(x) için p, Psi(p) için x bir sabit sayı olarak denkleme yazılmak zorunda.
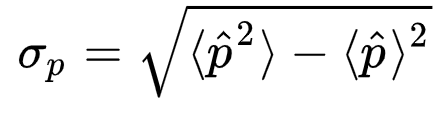
Psi(x) için standart sapmaya tekrar bakalım. Eğer burada p bir dağılım değil sabit bir sayıysa standart sapma sıfır gelecek. E ama bunun Heisenberg belirsizlik ilkesine göre x’in standart sapmasını sonsuz yaptıracağını biliyoruz. Bir şeyin standart sapmasının sonsuz olmasıysa biz nereyi x=0 seçersek seçelim parçacığın sonsuz uzayın herhangi bir yerinde eşit olasılıkla görülebilmesi demek. Yani bizim p momentumuna sahip bir parçacığımız var dediğimiz an o parçacık uzayın tamamında görülebilir. Bizim x pozisyonunda bir parçacığımız var dediğimizdeyse o parçacık sıfırdan sonsuza tüm momentum değerlerinde olabilir.
Psi(x) bize p momentumuna sahip bir parçacığın nerede olacağının olasılık genliğini verir — herhangi bir yerde olabilir!
Psi(p) bize x pozisyonundaki bir parçacığın hangi momentuma sahip olacağının olasılık genliğini verir — herhangi bir momentumda olabilir!
O zaman bu herhangi bir kuantum parçacığının yerini biliyorsak her hızda olabilir, hızını biliyorsak herhangi bir yerde olabilir mi demek? Hayır, çünkü hatırlayın bu Psi(x) denklemini yazarken serbest uzayda, hiçbir kuvvetin etkisi altında olmayan bir parçacık tanımlamıştık. Oysa fiziksel parçacıklar her daim fizik kanunlarıyla dikte edilmiş kuvvetlerin etkisi altındadır. İşte kuantum mekaniği de burada başlar, çeşitli fiziksel kuvvetler altında sistemlerin (dalga-parçacık) davranışlarını inceler. Bunu da fiziksel niceliklere bağlı olan olasılık dağılımlarının genliklerini tasvir eden kuantum hallerini yazıp bu matematiksel tasvir üzerinde oynayarak yapar!
Kuantum Mekaniğine Giriş
Elimizdeki parçacığın yerini bulmaya çalışınca tüm uzayda çıktığı garip bir kuantum hal ile tatmin olmadığımızı düşünelim. Parçacık mutlaka elimizin içinde olsun istiyoruz, bu nedenle de parçacığın çevresinde elimizi yumruk yaptık. Şu an biliyoruz ki bu parçacık kesinlikle avcumuzun içinde! Ancak artık yukarıda yazdığımız basit Psi(x) fonksiyonu bu parçacığın fiziksel durumunu tasvir etmek için yeterli değil. Peki o zaman yeni, avcumuzun içindeki parçacığın özelliklerini tasvir eden Psi(x) fonksiyonumuzu nasıl bulacağız?
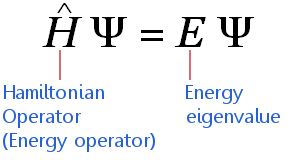
Schrödinger denklemi denilince uzun ve karmaşık formüller görürsünüz, ancak aslında işin özünde denklem yukarıdaki haliyle bize çok şey söyler. En soldaki şapkalı H bir Hamiltonian operatörü, yani sizin sisteminizi etkileyen tüm fiziksel kuvvetleri tasvir eden ‘şey’. İşte ‘avcunuzu kapama’ fiziksel eyleminin matematiksel karşılığı bu şapkalı H’nin bir yerinde tasvir edilecek.
Kuantum fiziği dersi almış olanlar şu an nereye gittiğimi anlayacaklar, bu problem aslında ‘kutuda parçacık (particle in a box)’ problemidir. Elimdeki küçük parçacık için avcumu ‘geçilemez’ bir engel olarak alırsam — yani potansiyel enerjisi sonsuz bir duvar gibi düşünürsem — parçacık mutlaka avcumun içinde kalmak zorunda olacaktır.
Hamiltonian operatörünün iki parçası vardır, kinetik enerji ve potansiyel enerji. Kinetik enerji parçacığın momentumuna bağlıdır, potansiyel enerjiyse içinde bulunduğu fiziksel ortamın özelliklerine. Mesela ortamda bir elektromanyetik alan varsa bunun sizin parçacığınızın üzerine etkisini operatörün potansiyel enerji kısmına yazarsınız. Aynı biçimde ortamda parçacığın geçmesini önleyen sonsuz enerjili duvarlar varmış gibi düşündüğünüz bir durumda da (mesela avcunuzu kapadınız ve parçacık içinde) bunu potansiyel enerji kısmında tasvir edersiniz.
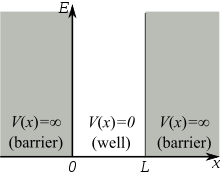
Yani kapalı avcumuzdaki bir parçacığın enerjisine bağlı olarak nerede bulunabileceğine dair matematiksel gösterim için bulacağımız Psi(x)’i yukarıdaki resme indirgedik. İki taraftaki bariyerler avcumuzu temsil ediyor, ortadaki serbest alansa avuç içimizdeki boşluğu. Bu elbette tek boyutlu bir gösterim, ancak bunu x,y,z için ortak şekilde yaparsanız üç boyutlu bir gösterim de elde edebilirsiniz (tabi o zaman avuç içimizin küp şeklinde olduğunu varsaymış oluruz, daha gerçekçi bir yaklaşım için küresel koordinat sisteminde çözmek gerekir ama o biraz daha ileri bir matematik gerektirmekte).
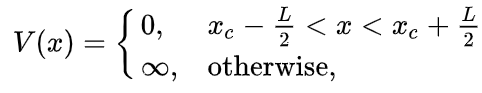
H operatörünün iki kısmı olduğunu söylemiştik, kinetik ve potansiyel enerjiye tekabül eden kısımlar. Yine liseden hatırlarsınız, parçacıkların kinetik enerjisi mv²/2 olarak tanımlanır. E ama biz momentumla (yani p=mv ile) çalışıyoruz, o zaman kinetik enerjimiz p²/2m olur. Potansiyel enerji olarak da yukarıdaki fonksiyonu kullanalım, yani avcumuzun içinde kalan x değerleri için potansiyel 0 iken kalan her yerde sonsuz potansiyel enerjili bir alan tanımlayalım. Bu da aslında şu demek, genel geçer bir kural olarak eğer bir parçacığın enerjisi bir alanın potansiyel enerjisinden düşükse o parçacık o alana giremez (bazı istisnalar var, göreceğiz). Eğer bir alanın potansiyel enerjisi sonsuzsa oraya kesinlikle hiçbir parçacık giremez. Bizim de zaten istediğimiz buydu, parçacığımız avcumuzun dışına çıkamasın. O zaman yukarıdaki denklem ne hale geldi diye bakacak olursak elde ettiğimiz denklem şuna benzeyecek:
(Kinetik enerji operatörü) Psi(x) + (Potansiyel enerji operatörü) Psi(x) = (Enerji) Psi(x)
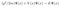
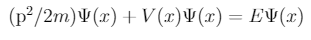
Yukarıdaki V(x) tanımımızı hatırlayın, sonsuz olduğu yerler vardı. Enerjisi sonsuz olmayan parçacıklar bu alanda var olamaz demektir bu. Enerjisi sonsuz olan parçacık da olamayacağına göre yukarıdaki denklemde sonsuz V(x)’e tekabül eden bir Psi(x) olamaz (tersi de mümkün, Psi(x)’in mutlaka sıfır olması gerektiğini matematiksel olarak gösterip de “böyle bir durum mümkün değildir” diyebilirsiniz). O zaman elimizdeki denklem baya basit bir şeye indirgendi gibi duruyor, x sadece avcumuzun içindeki değerleri alabilirken V(x) = 0 olacağından ötürü alttaki formu elde ediyoruz.
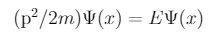
Buradaki p aslında şapkalı p olacak, yani bir operatör. Momentum operatörü.

Tipi garip geliyor olabilir ama hatırlayın momentum hız çarpı kütleydi, e hız zaten pozisyonun zamana göre değişimi demek. Eksi i ve Planck sabitiyle çarpınca bize kuantum mekaniksel momentum operatörünü veriyor. Daha da uzatmadan sadede gelelim:
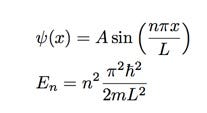
Psi(x) yukarıdaki denklemin çözümünde bir sinüs fonksiyonu çıkıyor. Buna bağlı olan enerji seviyeleriyse gördüğünüz n’ye bağlı şekilde beliriyorlar. İşte bu, kuantum mekaniğinin gerçekten kuantum mekaniği olduğu yer.
Şimdiye kadar size kuantum mekaniğinin kesikli olduğunu söyleyip sonra hep sürekliliği olan Psi(x)’lerle iş yaptırdım, ‘kuantum’ bunun neresinde diye bazılarınızın aklından geçmiş olabilir. Kuantum mekaniğindeki kesiklilik kuantum hali anlatan dalga fonksiyonunda değil, Schrödinger denkleminin çözümlerinde çıkıyor! Elimizin içinde kendi halinde bir parçacık var, avcumuzu kapattık, parçacık kendi halindeyken tüm uzayda eşit olasılıklarla ve istediği enerji düzeyinde bulunabilen, kırlarda özgürce koşan Heidi’ydi. Avcunuzu kapatıp onu bir alan hapsettiğinizde ise bir anda tüm özellikleri ’n’ye bağlı hale geldi.
Burayı anlamak önemli, bu denklemdeki n ancak pozitif tam sayı değerleri alabilen bir parametre. Yani n=0,1,2,3,4… diye gidiyor ve bunlar da tam olarak kuantum mekaniğine dair duymuş olabileceğiniz ‘enerji seviyeleri’ne tekabül ediyorlar. Şimdi biraz daha dikkatle enerji sonucunu inceleyelim.

Avcunuzun içindeki parçacığın enerji düzeyleri üç parametreye bağlı, π ve 2 bildiğimiz sayılar, çizikli h ise Planck sabiti (yani o da birimi olan sabit bir sayı aslında). Bu parametreler n, m ve L. Yukarıdan hatırlayın, L kutumuzun boyuydu, bizim örneğimizde avcumuzun içinin bir uçtan diğerine genişliği diyebiliriz. Diğer parametremiz m ise parçacığın kütlesi. Son parametremiz ise n, yani enerji seviyeleri. Burada m ve L standart kuantum fiziği için istediğiniz değeri alabilir, ancak n mutlaka pozitif tam sayı olmak zorunda.

Farklı enerji seviyeleri için Psi(x)’leri yukarıda görebilirsiniz. Bunların kareleri parçacığı avcunuzun içinde nerede bulabileceğinizi gösteren f(x) olasılık dağılımı fonksiyonlarını verecekler. Şimdi yukarıdaki resimlerin ne kadar garip ve beklenmedik olduğuna dair birkaç şey söyleyelim. n=1 için hayat normal gibi, yani parçacık yüksek ihtimalle ortada, daha düşük ihtimalle biraz ortaya yakın, en düşük ihtimalle duvarlara yakın; bildiğimiz normal dağılım. Ama n=2 için parçacığın ortada bulunma ihtimali sıfır! Düşünün avcunuzun içinde oradan oraya çarpan bir parçacık var ama milyonlarlca ölçüm alsanız bile tam ortada asla göremiyorsunuz. Aynı durum daha yüksek enerji düzeylerinde de geçerli, parçacığı bazı kesikli değerlerde görme ihtimaliniz sıfır.
Bu klasik mekanikle bağdaşan bir fiziksel tasvir değil. Sonuçta parçacık avcumuzun içinde oradan oraya sekiyorsa mutlaka ortadan da (hatta çizgi üzerindeki her noktadan) geçmek zorunda. Dolayısıyla da her yerde bulunabilme ihtimali olmalı. Oysa kuantum mekaniksel bir tasvir bize, çeşitli enerji seviyelerinde parçacığın çeşitli yerlerde olamayacağını gösteriyor. Basitçe, klasik ve kuantum mekanik bize aynı sistemin (avcumuzun içinde bir parçacık) nasıl davranacağına dair farklı fiziksel öngörülerde bulunuyorlar. Peki bunun arkasındaki matematik nereden geliyor?
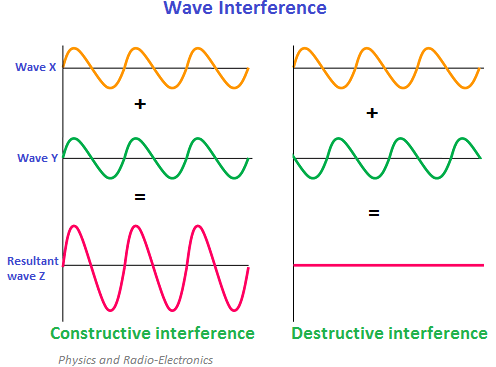
Daha önce klasik mekanikte olasılık dağılımlarına, kuantum mekaniğinde ise olasılık dağılımlarının kareköklerine baktığımızı söylemiştik. Bu karekökü meselesi, yani matematiksel alet çantamıza kompleks sayıları ve negatif olasılıkları dahil etme yetkinliği, kuantum mekaniğinin matematiğinin temelini oluşturuyor. Yukarıda dalga girişim modellerini görüyorsunuz. Eğer iki dalga uyumlu bir şekilde üst üste gelirlerse bunlar ‘yapıcı girişim’ gerçekleştirir ve dalgalar güçlenir, eğer uyumsuz şekilde üst üste gelirlerse ‘yıkıcı girişim’ gerçekleştirirler ve dalgalar sönümlenir.

Daha iyi anlamak için tekrar kosinüs fonksiyonuna bakalım. Olasılık dağılımları buradaki kırmızı cos²(x) dalgası gibi davranırlar, hep 0 ila 1 arasında değerlere sahiptirler. Dolayısıyla yalnızca ‘yapıcı girişim’ yapabilirler. Bunların karekökleri ise mavi cos(x) dalgası gibi davranabilirler, yani negatif değerleri de olabilir, bu da onların ‘yıkıcı girişim’ de yapabilmesine olanak sağlar. Bu nedenle bir parçacığın ‘olası’ iki farklı olasılık dağılımı fonksiyonu varsa bu farklı ‘olasılık’ fonksiyonları üst üste binerek ‘toplam’ veya bir nevi ortalama olasılık fonksiyonunu etkilerler. Çift yarık deneyini tekrar hatırlayalım.

Tek yarıkta elimizde bir normal dağılım vardı. Sağ üstteki iki ‘normal’ dağılımın birleşimi. Burada soldaki gibi iki tane fonksiyonun yan yana olduğunu görmek mümkün, bir nevi çift hörgüç oluşturuyorlar, bunun nedeni de yapıcı girişimde bulunmaları. Oysa sağ alttaki resim daha çok daha farklı, çünkü burada olasılık dağılımının karekökleri (kuantum hali tasvir eden dalga fonksiyonunun) bazı noktalar için ‘yıkıcı girişim’ gösteriyor, biri +0.5’ken diğeri -0.5 oluyor ve toplamları 0 veriyor, parçacık ise 0 olasılık olan yere düşmüyor.

Parçacıkların üstteki gibi dalgaların alttaki gibi gitmesi beklenirken kuantum sistemlerde parçacıklar da alttaki gibi gidiyor. Hatırlayın, fizik bilimi için “…bir sistemin matematiksel tasvirini çıkarmak, sonrasında bu matematiksel tasvir üzerinde fiziksel dünyada karşılığı olduğunu varsaydığımız operasyonları uygulamak, sonucunda çıkan matematiksel tasvirin fiziksel gerçekliğini test etmek” demiştik. Klasik fiziksel matematiksel tasvir bize üstteki resmin doğru olduğunu, kuantum mekaniksel tasvir ise alttakinin doğru olduğunu söylüyor. Deney yaptığımızda görüyoruz ki küçük parçacıklar için (elektron gibi) alttaki, büyük parçacıklar için (karmaşık moleküller gibi) üstteki doğru. Yani dünya, mikro ve makro düzeylerde (çok küçük ve büyük) farklı matematiksel tasvirlere sahip!
Toparlarsak
Bu uzun yazıda sıfırdan başlayıp çok basit kuantum mekaniksel problemleri tasvir edip çözme aşamasına kadar geldik. Peki bu süreçte bize nelerin lazım olduğunu gördük?
Öncelikle, temel matematiksel yetilerimizin gelişmiş olması gerektiği açık. Fonksiyon, olasılık, vektörel gösterimler, diferansiyel denklemler gırla havada uçuşuyor. Ancak daha kesin konuşmak gerekirse dört temel ayaktan bahsedebiliriz; olasılık, kalkülüs, diferansiyel yöntemler, lineer cebir. Bunları yalayıp yutmuş olmanıza gerek yok, fakat en azından gösterimlerini, temel aksiyomlarını bilmek gerekli (mesela olasılık toplamı 1 eder, türev-integral neden öyle şeyler, lineer ne demek, kompleks sayılarla nasıl çalışılır).
İkinci olarak, biraz fizik de bilmeniz önemli. Pozisyon, momentum, enerji gibi kavramların en azından neye tekabül ettiklerini bilmeden çoğu şey anlamsız kalacaktır. Ayrıca boyutlar üzerine düşünebilme algısı da klasik ve kuantum mekaniğinin farkını anlamak için önemli. Planck sabiti 10 üzeri eksi 34 Joule çarpı saniye, mesela bu ne demek? Küçük gibi duruyor ama ne kadar küçük? Ben elime pinpon topu alıp bunu çevirsem mesela kaç Planck sabiti kadar açısal momentumu olur? Gibi soruları direk yanıtlayamayacak olsanız da süre verildiğinde (mesela bir sınav sorusu gibi sorulduğunda) yanıtlayabilecek olmanız kuantum mekaniğini kafanızda oturtmanıza yardımcı olur.
Bu yazıda elbette atladığımız çok şey var. Örneğin commutativity (sırabağımlılık) ve ölçüm problemi gibi daha giriş dersinin başlarında işlenen konulara hiç değinmedik. Atomik sistemlerde kuantum mekaniğinin kullanımına, lazerlere, MR cihazlarının çıkışına sebep olacak olan osilasyon tasvirlerine de girmedik. Kuantum mekaniği oldukça geniş ve zengin bir alan, bu yazıda vermeye çalıştığımız şeyin kapsamıysa oldukça dar ama net; bu Psi(x) ile neyi anlamaya ve tasvir etmeye çalışıyoruz? Eğer bunu öğrendiyseniz yazı işlevini yerine getirmiş demektir!
- Konuya popüler olarak devam etmek isteyenler için YouTube’da pek çok video mevcut. Biraz daha ciddi ilgileniyorsanız yazılı kaynaklara gitmenizi ve elinize kağıt kalem alıp en azından basit soruları çözmeyi denemenizi tavsiye ederim, kağıt kalemle sorulara girişmeden (elinizi kirletmeden) bu meretin matematiği ne yazık ki öğrenilemiyor.
- Akademik olarak ilgileniyorsanız Coursera, edX gibi yerlerde pek çok ders var — ayrıca çoğu kitabın PDF’ini online bulabilirsiniz (mesela Griffiths-Introduction to Quantum Mechanics).
Zaman içerisinde yazının bu kısımlarına daha detaylı bir kaynakça ve yol-yordam haritası da eklenebilir.
Bitirirken not: Koronadan evlere tıkıldığımız şu günlerde dilerim kafanızı yeteri kadar meşgul edecek bir dikkat dağınıklığı yaratabilmişizdir. Her türlü yorum ve katkınız için zeki.seskir@gmail.com adresine yazabilirsiniz.









Yoruma kapalı.