Verimli algoritma arayışı, bilgisayar bilimlerinde önemli bir etkiye sahiptir. Bir veritabanı içinde belirli bir öğeyi bulma problemi, N öğeden oluşan sıralanmamış bir veritabanı için temel bir zorluktur. Geleneksel hesaplama yöntemlerinde, bu görev genellikle O(N) zaman karmaşıklığı ile gerçekleştirilir ve doğrusal arama işlemi kullanılır. Ancak kuantum mekaniğinin ilkelerini temel alan kuantum hesaplama paradigması ve Lov Grover tarafından ortaya atılan Grover algoritması, bu soruna potansiyel bir çözüm getirmiştir. Grover algoritması, kuantum hesaplama alanında bir dönüm noktası olarak 1996 yılında ortaya çıkmıştır. Hint asıllı Amerikalı bir bilgisayar bilimcisi olan Lov Grover, kuantum bilişimin yapılandırılmamış veritabanı arama konusundaki benzersiz potansiyelini fark ederek, kuantum bilişim alanında önemli bir algoritma geliştirmiştir.
Grover’ın algoritması, bilgi işleme alanında karmaşık senaryoların çözümüne yöneliktir. Yapılandırılmamış veriler arasında arama yapma sorununu ele alır ve kuantum bilgisayarlarının üstünlüğünü kullanarak bu probleme çözüm getirir.
Aşağıdaki diyagramda gösterildiği gibi, N sayıdan oluşan sıralanmamış bir listede bazı benzersiz özelliklere sahip olan w değerini (Kırmızı Kutu) bulmak istediğinizi varsayalım. Peki, w değerini nasıl bulabilirsiniz?

Klasik Yaklaşım: Klasik hesaplama yöntemlerinde, listedeki bu öğelerin ortalama N/2’sini kontrol etmemiz gerekir. Basit bir ifadeyle, her birini tek tek doğrulamanız gerekir, bunun için N adım, yani O(N), gerekir. Sıralı veriler üzerinde ikili aramayı uygulamak için rastgele erişim ve ön sıralama eklenirse, log(N) adım, yani O(log(N)), gerekir. Ancak, bir kuantum algoritması kullanmak kabaca √N adım gerektirir. Örneğin, 25 elemanlı bir liste alalım ve listeden bir değer aramak istiyoruz, klasik olarak N adım sürecektir. Kuantum algoritması ile √N adım sürecektir, yani klasik olarak 25 adımda problem çözerken, kuantum algoritması ile kuadratik olarak √25=5 adımda problem çözmüş olacağız.
Peki problemimizi tanımladıktan sonra ne yapacağız? Şimdi adım adım problem çözmek için gerekli adımları yapalım. İstediğimiz elemanı veya değeri ararken Genlik Yükseltme prosedürü büyük bir öneme sahiptir. Bu prosedür, aranan değerin olasılık genliğini artırırken diğer olasılık genliklerini azaltarak arama sürecini optimize eder. Düşünelim ki dengeli bir süperpozisyonda (k1, k2, k3,…kn) bulunan kw değerini yakalamak istiyoruz. Genlik amplifikasyonu işlemi, bu süperpozisyondaki kw ketini diğerlerinden ayırmak için kullanılır.
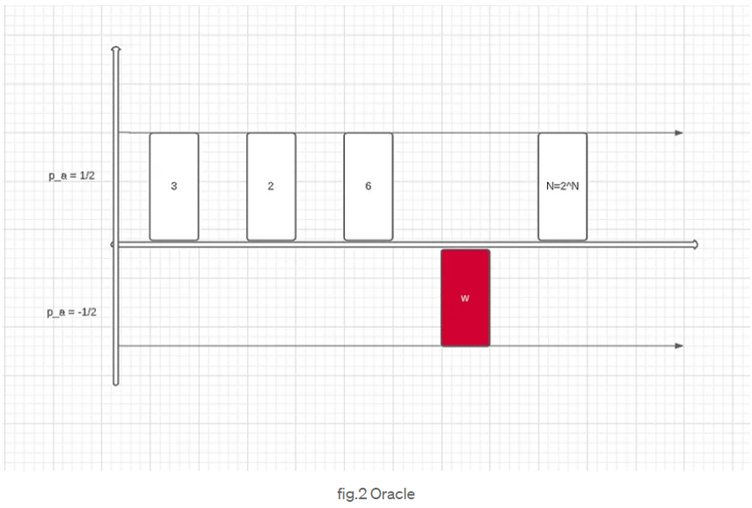
Bu prosedürde, kw’nin genliğini artırmak için özel bir kahinden (oracle) faydalanılır. Kahin, kw’yi temsil eden kete negatif bir faz ekleyerek onu diğer ketlerden ayırt etmeyi sağlar, yani ilk kahinimiz budur. Genlik amplifikasyonu süreci, aranan değeri bulmak için kuantum algoritmalarında önemli bir adımdır. Belirlenmiş bir kahin, aradığımız değeri diğerlerinden ayırarak istenen sonuca daha hızlı ve etkili bir şekilde ulaşmamızı sağlar.
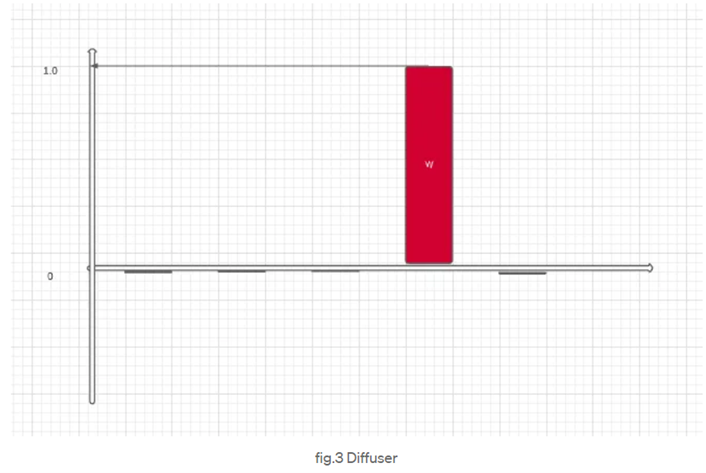
İkinci kahin, hedef kübitin (kw) tüm genliğini tersine çevirir. Bu kahin, hedef kübit dışındaki durumların genliğini sıfıra indirerek, hedef kübiti belirlememize yardımcı olur. Hedef kübitin genliğini tersine çevirmek, diğer durumların genliğini sıfıra indirerek aranan değeri belirgin hale getirir. Bu kahin, arama sürecinde hedef kübitin belirlenmesine odaklanarak kuantum arama algoritmalarında önemli bir adımı oluşturur. Son aşamada, ikinci kahinden gelen durumlar, listedeki öğe ile ilgili kodlanmış değerlerle karşılaştırılır ve ölçülür. Elde edilen sonuç, veritabanındaki bilgi ile eşleştirilir. Eğer elde edilen cevap yanlışsa, adımlar tekrarlanır. Bu durumda, hata olasılığı O(1/N) seviyesindedir. İkinci oracle’den gelen durumların karşılaştırılması, aranan öğeyi belirlemek için kuantum arama sürecinde son derece kritiktir. Yanlış cevap alındığında tekrar adımlara başvurarak, arama işleminin doğruluğunu artırmak amaçlanır. Hata olasılığının O(1/N) seviyesinde olması, kuantum algoritmalarının doğruluğunu ve etkinliğini vurgular.
Grover Algoritmasının Sınırlamaları
İkinci Dereceden Hızlanma: Grover’ın algoritması, klasik algoritmalara göre ikinci dereceden bir hızlanma sağlar. Bu, özellikle büyük arama uzayları için önemli bir avantajdır. Ancak daha küçük arama uzayları için aynı ölçüde etkili olmayabilir. Bu durum, algoritmanın küçük ölçekli problemlerde beklenen performansı gösteremeyebileceği anlamına gelir.
Donanım ile Sınırlıdır: Grover’ın algoritması, belirli bir hızlanma seviyesine ulaşabilmek için çok sayıda kübit kullanılmasını gerektirir. Bu, mevcut kuantum donanım teknolojisinin sınırlarının ötesine geçer. Dolayısıyla, algoritmanın pratik kullanımı için daha güçlü ve geniş kapsamlı kuantum donanımlarının geliştirilmesi gerekmektedir.
Hata Eğilimli: Kuantum algoritmalarının genel bir özelliği olan gürültü ve tutarsızlık, Grover’ın algoritmasını da etkileyebilir. Bu hatalar, algoritmanın doğruluğunu ve güvenilirliğini azaltabilir. Gerçek dünya uygulamalarında, bu tür hataların etkisi algoritmanın pratik kullanımını sınırlayabilir ve güvenilirliğini azaltabilir. Bu sınırlamalar, Grover’ın algoritmasının henüz geniş ölçekte pratik uygulamalarda kullanımını kısıtlayabilir. Ancak, ilerleyen kuantum teknolojileri ve hata düzeltme teknikleriyle birlikte bu sınırlamaların aşılması beklenmektedir.
Grover Algoritmasının Uygulamaları
Veri Madenciliği: Grover’ın algoritması, klasik bilgisayarlarla bulunması zor veya imkansız olan büyük veri kümelerindeki modelleri bulmak için kullanılabilir. Örneğin, finansal veri tabanlarında hileli işlemleri tespit etmek veya tıbbi görüntülerdeki kanser hücrelerini tanımlamak gibi alanlarda kullanılabilir.
Kriptografi: Grover algoritması, şu anda güvenli olarak kabul edilen kriptografik anahtarlar kırmak için kullanılabilir. Bu, çevrimiçi iletişimlerin ve işlemlerin güvenliği üzerinde büyük bir etkiye sahiptir. Kuantum bilgisayarlarının gelişmesiyle, klasik kriptografinin zayıf yönlerini hedef alabilir ve güvenlik standartlarını değiştirebilir. Bu uygulama alanları, Grover Algoritması’nın gelecekte büyük bir etki yapabileceği önemli alanlardır. Ancak, pratik uygulamalara geçmeden önce kuantum bilgisayarlarının donanım yetenekleri ve hata düzeltme teknolojileri gibi alanlarda daha fazla gelişme kaydetmesi gerekebilir.
Sonuç
Genel olarak, Grover’ın algoritması çeşitli problemlerin üstesinden gelmek için güçlü bir araç olarak kullanılabilir. Örneğin, veri içerisindeki modelleri bulma, kriptografik anahtarları kırma ve optimizasyon problemlerini çözme gibi alanlarda etkilidir. Kuantum bilgisayarlarının güçlenmesiyle birlikte, Grover’ın algoritması giderek daha fazla önem kazanacaktır
Yazar: Mert Çelik
Redaktör: Uzay Nağme Oruz









