Kuantum yaklaşık optimizasyon algoritması (QAOA), kontrol parametreleri klasik olarak optimize edilmiş hibrit bir algoritmadır. Varyasyon parametrelerine ek olarak herhangi bir optimizasyon modelinin performansını iyileştirmek için doğru hiperparametre seçimi çok önemlidir. Kontrol derinliği veya değişken parametrelerin sayısı, QAOA için en önemli hiperparametre olarak kabul edilir.
Physical Review A’da yayınlanan makaleye göre, proksimal gradyan inişine dayalı otomatik bir algoritma ile kontrol derinliği seçimi araştırılıyor. Otomatik algoritmanın performansı, yedi düğümlü ve on düğümlü “Max-Cut” problemlerinde gösterilmektedir. Bu performanslar, yineleme sırasında kontrol derinliği önemli ölçüde azaltılabileceğini ve yeterli düzeyde bir optimizasyon doğruluğu elde edileceğini göstermektedir. Teorik yakınsama garantisi ile önerilen algoritma, rastgele arama veya ampirik kuralların yerine uygun kontrol derinliğini seçmek için verimli bir araç olarak kullanılabilir. Ayrıca, kontrol derinliğinin azaltılması, bir devredeki kuantum kapılarının sayısında önemli bir azalmaya neden olacak ve bu da QAOA’nın gürültülü orta ölçekli kuantum cihazlarında uygulanabilirliğini iyileştirecektir.
Max-Cut problem
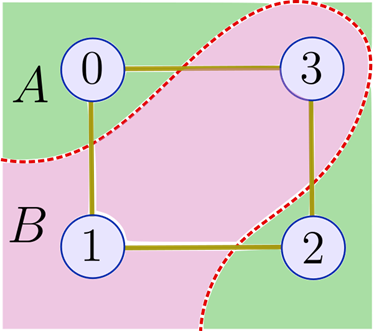
Max-Cut’un amacı, bir grafikteki köşelerin belirli bir bölümü (mavi daireler) tarafından iki küme halinde “kesilen” kenarların (sarı çizgiler) sayısını maksimize etmektir (aşağıdaki şekle bakınız).
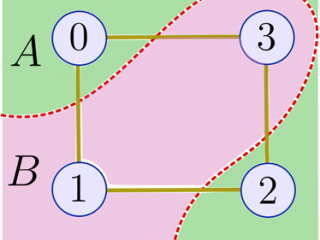
m kenarları ve n köşeleri olan bir grafik düşünün. Köşelerin z bölümünü A ve B olmak üzere iki kümeye ayırıyoruz.
Burada C, kesilen kenarları sayar. z bir tepe noktasını A kümesinde; diğerini B kümesinde αth kenarından yerleştirirse, Cα(z)=1 ve aksi takdirde Cα(z)=0. Mümkün olan maksimum C değerini veren bir kesim bulmak tam bir NP* problemidir, bu nedenle bir polinom zaman algoritması için en iyi beklentimiz yaklaşık bir optimizasyonundan beklenmektedir. Max-Cut’ın durumunda, C(z) için olası maksimum değere yakın bir değer veren bir z bölümü bulmak anlamına gelir.
NP*- nondeterministic polynomial belirlenebilir, tanımlanabilir olmayan polinom (Matematikte, bir polinom belirli sayıda bağımsız değişken ve sabit sayıdan oluşan bir ifade).
–
Yazar: Hüseyin Türker
Editör: Damla Gözük








Yoruma kapalı.