Kuantum Mekaniği Nedir?

Kuantum mekaniği oluşmaya başladığı ilk zamanlardan bu yana fiziksel dünyayla ilgili düşüncelerimizin farklılaşmasına sebebiyet vermiştir. Bu içerik kuantum mekaniğinin ne olduğuna, kuantum mekaniğinin temel ilkelerine kısaca değinmektedir. Kuantum mekaniği (Quantum mechanics; kuantum fiziği, kuantum teorisi, dalga mekanik modeli ve matris mekaniği olarak da bilinir), kuantum alan teorisi de dahil olmak üzere, fizikte doğanın özelliklerini atomik ölçekte tanımlayan temel bir çerçeve ve teoridir. Diğer bir şekilde söylenecek olursak; kuantum mekaniği, belirsizlik ilkesine tabi olan atom, molekül ve diğer fiziksel sistemlerin mekanik teorisidir.

Klasik fizik ise, görelilik teorisinin ve kuantum mekaniğinin formülasyonundan önce var olan fiziği tanımlamaktadır. Doğanın makroskopik ölçekte birçok yönüne açıklama getir ve formüle eder. Kuantum mekaniği ise, büyük ölçeklerde doğa yasalarını açıklamanın haricinde bu tanımı küçük (atomik ve atom altı) ölçeklere genişletir.

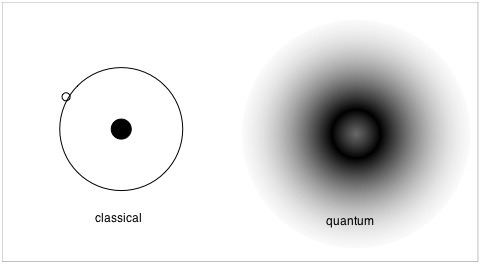
Atomik ve atom altı ölçeğinde, nesnelerin günlük boyutlarda ve hızlarda nasıl hareket ettiğini tanımlayan klasik mekaniğin denklemlerinin çoğu yararlı olmaktan çıkar. Klasik mekanikte, nesneler belirli bir zamanda belirli bir yerde bulunur. Bununla birlikte, kuantum mekaniğinde, nesneler bunun yerine bir olasılık bulanıklığında bulunur; nesnelerin hem A noktasında olma şansları, hem de B noktasında olma şansları da vardır.

Klasik fizikteki teorilerin çoğu ölçekte geçerli bir yaklaşım olarak kuantum mekaniğinden türetilebilir. Kuantum mekaniği; enerji, momentum, açısal momentum ve bağlı bir sistemin diğer miktarlarının ayrık değerlerle (nicemleme) sınırlandırılması, nesnelerin hem parçacıkların hem de dalgaların (dalga-parçacık ikiliği) özelliklerine sahip olması ve sınırları olması nedeniyle klasik fizikten oldukça farklıdır.

Kuantum mekaniği, Max Planck’ın 1900 yılındaki çözümünde olduğu gibi klasik fizik ile uzlaştırılamayan gözlemlerin, Albert Einstein’ın fotoelektrik Albert Einstein’ın 1905 makalesinde enerji ve frekans arasındaki iletişimi açıklamasının ardından yavaş yavaş ortaya çıkmıştır. Ancak erken kuantum teorisi 1920’li yılların ortalarında Erwin Schrödinger, Werner Heisenberg, Max Born ve diğerleri tarafından derinlemesine olarak yeniden tasarlanmıştır.

Kuantum mekaniğinin gelişim sürecini Kuantum Mekaniğinin Kronolojisi yazımız aracılığıyla keşfedebilirsiniz.

Üç temel ilke

Kuantum mekaniği, klasik mekanik matematiğinin açıklayamadığı deneylerin bir dizi tartışmalı matematiksel açıklaması olarak başlayarak, onlarca yıl boyunca gelişti. 20. yüzyılın başında, Albert Einstein’ın görelilik teorisini, nesnelerin yüksek hızlarda hareketini tanımlayan ayrı bir matematiksel devrim olan görelilik teorisini yayınlamasıyla başladı. Bununla birlikte, göreliliğin aksine, kuantum mekaniğinin kökenleri herhangi bir bilim insanına atfedilemez. Daha ziyade, birden fazla bilim adamı, 1900 ve 1930 arasında giderek kabul gören ve deneysel doğrulama kazanan üç devrimci ilkenin temeline katkıda bulundu.

Niceliksel Özellikler

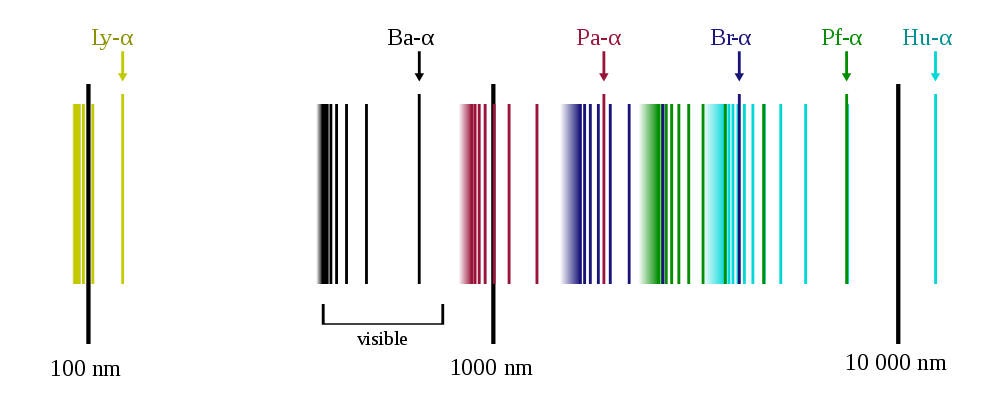
1900 yılında Alman fizikçi Max Planck, ampul filamanları gibi kırmızı-sıcak ve beyaz-sıcak nesnelerin parıltısında spektrumdan yayılan renklerin dağılımını açıklamaya çalıştı. Bu dağılımı tanımlamak için türettiği denklemin fiziksel anlamını verirken, Planck, sadece belirli renklerin (çok sayıda da olsa) kombinasyonlarının, özellikle de bazı temel değerin tam sayı katları olanların yayıldığını ima etti. Her nasılsa renkler nicelendi! Bu beklenmedik bir şeydi çünkü ışığın bir dalga gibi davrandığı anlaşılıyordu, yani renk değerleri sürekli bir spektrumda olmalıydı. Atomların bu tam sayı katları arasındaki renkleri üretmemesinin sebebi ne olabilirdi? Bu o kadar garip görünüyordu ki Planck nicemlemeyi matematiksel bir numaradan başka bir şey olarak görmedi. Ancak o dönemde herkes bu yanılgıya düşmüş durumdaydı.

Planck’ın denklemi, ileride kuantum mekaniğinin gelecekteki gelişimi için çok önemli olacak bir sayı da içeriyordu; o sayı, bu gün Planck sabiti olarak adlandırılmaktadır.

Nicemleme fizikteki diğer gizemleri açıklamaya yardımcı oldu. 1907’de Einstein, bir katının sıcaklığının neden farklı miktarlarda değiştiğini açıklamak için Planck’ın nicelik hipotezini kullandı.

1800’lerin başından beri, spektroskopi bilimi, farklı elementlerin “spektral çizgiler” adı verilen belirli ışık renklerini yaydığını ve emdiğini göstermiştir. Spektroskopi, uzak yıldızlar gibi nesnelerde bulunan elementleri belirlemek için güvenilir bir yöntem olmasına rağmen, bilim insanları her bir elementin neden bu belirli çizgileri ilk başta verdiğini merak etti. 1888’de Johannes Rydberg, hidrojenin yaydığı spektral çizgileri tanımlayan bir denklem elde etti, ancak kimse denklemin neden çalıştığını açıklayamadı. Bu, Niels Bohr’un Planck’ın nicemleme hipotezini Ernest Rutherford’un 1911 “gezegen” atom modeline uyguladığı zaman değişti.

Physics 2000’e (Colorado Üniversitesi’nden bir yayın) göre Bohr, elektronların bir atom çekirdeği etrafındaki “özel” yörüngelerle kısıtlandığını öne sürdü. Özel yörüngeler arasında “sıçrayabilirler” ve sıçramanın ürettiği enerji, spektral çizgiler olarak gözlenen belirli ışık renklerine neden olur. Niceliksel özellikler sadece bir matematik hilesi olarak icat edilmiş olsa da, o kadar iyi açıklama getirdiler ki kuantum mekaniğinin kurucu ilkesi haline geldiler.

Dalga-Parçacık İkiliği

1905 yılında Einstein, ışığın bir dalga olarak değil, bir tür “enerji kuantası” olarak hareket etmesini öngördüğü “Işığın Emisyonu ve Dönüşümü Hakkında Sezgisel Bir Bakış Açısı” başlıklı makalesini yayınladı. Einstein’ın önerdiği bu enerji paketi, özellikle bir atom, nicelenmiş titreşim hızları arasında “sıçrarsa” “sadece bir bütün olarak emilebilir veya üretilebilir” anlamına geliyordu. Bu aynı zamanda, birkaç yıl sonra gösterildiği gibi, bir elektronun nicelenmiş yörüngeler arasında “zıplaması” durumunda da geçerliydi. Bu model altında, Einstein’ın “enerji miktarı”, sıçramanın enerji farkını içeriyordu; Planck’ın sabitine bölündüğünde, bu enerji farkı, bu miktarların taşıdığı ışığın rengini belirledi.

Işığa göz atmanın bu yeni yolu ile Einstein, Planck’ın bir ampul filamanından yayıldığını tarif ettiği spesifik renkler de dahil olmak üzere dokuz farklı fenomenin davranışı hakkında bilgiler sundu. Ayrıca, belirli etkileşimlerin, “fotoelektrik etki” olarak bilinen bir fenomen olan elektronları metal yüzeylerden nasıl koparabileceğini açıkladı.

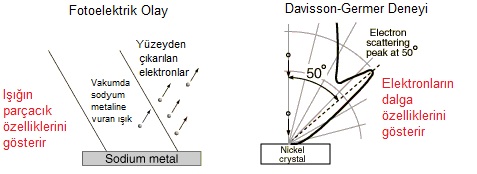
Einstein’ın bu keşfinden yaklaşık yirmi yıl sonra, “foton” terimi, bir elektron ışını tarafından dağılan ışığın renk değiştirdiğini gösteren Arthur Compton’un 1923 çalışması sayesinde enerji miktarını tanımlamak için popüler hale geldi. Bu, ışık parçacıklarının (fotonlar) gerçekten parçacıklarla (elektronlar) çarpıştığını ve böylece Einstein’ın hipotezini doğruladığını gösterdi. Bu sayede, ışığın hem dalga hem de parçacık olarak davranabileceği ve ışığın “dalga-parçacık ikiliği” nin doğrulanarak kuantum mekaniğinin temeline oturtulabileceği anlaşıldı.

Maddenin Dalga Özelliği

1896’da elektronun keşfinden bu yana, tüm maddelerin parçacıklar şeklinde var olduğuna dair kanıtlar yavaş yavaş inşa ediliyordu. Yine de, ışığın dalga-parçacık ikililiğinin göstermesi, bilim insanlarına maddenin sadece parçacık olarak hareket etmekle sınırlı olup olmadığını sorgulattı. Belki de dalga-parçacık ikiliği madde için de geçerli olabilirdi?

Bu muhakemeyle önemli ilerleme kaydeden ilk insanı, Louis de Broglie adında bir Fransız fizikçiydi. 1924 yılında de Broglie, parçacıkların dalga benzeri özellikler gösterebileceğini ve dalgaların parçacık benzeri özellikler gösterebileceğini göstermek için Einstein’ın özel görelilik teorisinin denklemlerini kullandı. Daha sonra 1925’te bağımsız çalışan ve ayrı matematiksel düşünme çizgilerini kullanan iki bilim insanı, de Broglie’nin denklemlerini elektronların atomlarda nasıl dolaştığını açıklamak için (klasik mekanik denklemleri kullanılarak açıklanamayan bir fenomen) uyguladı. Almanya’da fizikçi Werner Heisenberg (Max Born ve Pascual Jordan ile birlikte) bunu “matris mekaniği” geliştirerek başardı. Avusturyalı fizikçi Erwin Schrödinger, “dalga mekaniği” adlı benzer bir teori geliştirdi. Schrödinger 1926’da bu iki yaklaşımın eşdeğer olduğunu gösterdi (İsviçreli fizikçi Wolfgang Pauli, Jordan’a matris mekaniğinin daha eksiksiz olduğunu gösteren yayınlanmamış bir sonuç gönderdi).

Her bir elektronun Rutherford-Bohr modelinin yerini bir atom çekirdeği etrafında bir dalga (bazen “bulut” olarak da anılır) olarak gördüğü Heisenberg-Schrödinger atom modeli oluşuyordu. Yeni modelin şartlarından biri, bir elektron oluşturan dalganın uçlarının buluşması gerektiğiydi. Bu şartın bir sonucu, sadece bazı sayılarda kret ve bretlere izin verilmesidir, bu da bazı özelliklerin neden nicelendirildiğini açıklamaktadır.

Atomun Heisenberg-Schrödinger modelinde, elektronlar yörüngelerden ziyade bir “dalga fonksiyonuna” uyar ve “orbitalleri” işgal eder. Rutherford-Bohr modelinin dairesel yörüngelerinden farklı olarak, atomik orbitaller değişen çeşitli şekillere sahiptir.

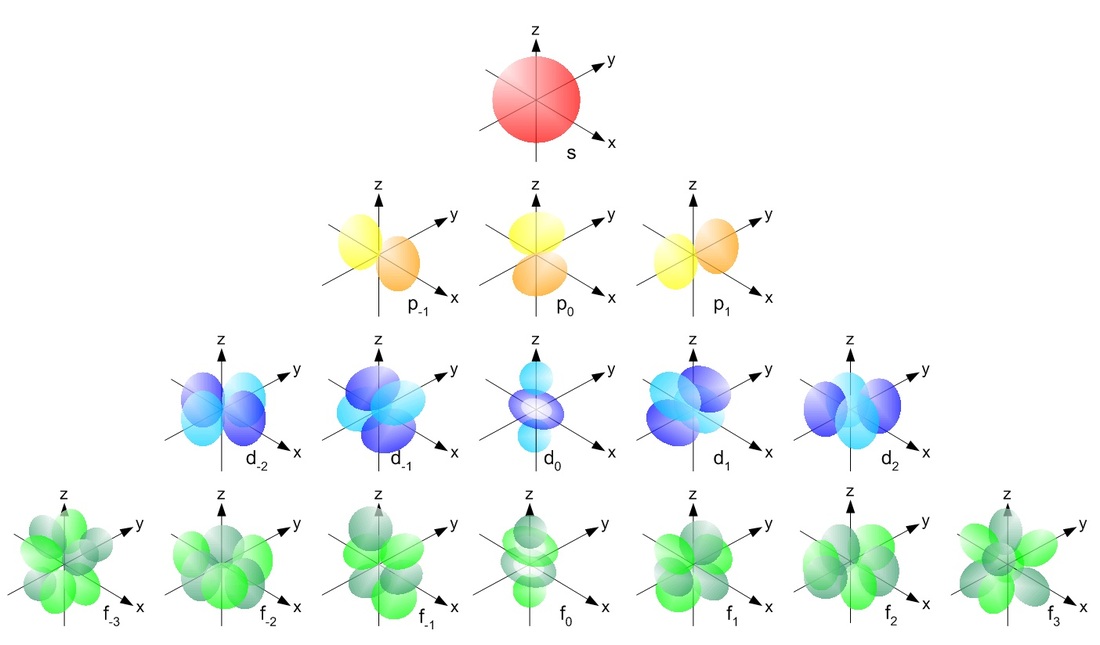
1927’de Walter Heitler ve Fritz London, atomik orbitallerin moleküler orbitalleri oluşturmak için nasıl birleşebileceğini göstermek için atom mekaniğini geliştirdiler ve atomların molekülleri oluşturmak için neden birbirlerine bağlandığını etkili bir şekilde gösterdiler. Bu, klasik mekaniğin matematiği kullanılarak çözülemeyen başka bir sorundu. Bu anlayış “kuantum kimyası” ise alanına yol açtı.

Belirsizlik ilkesi

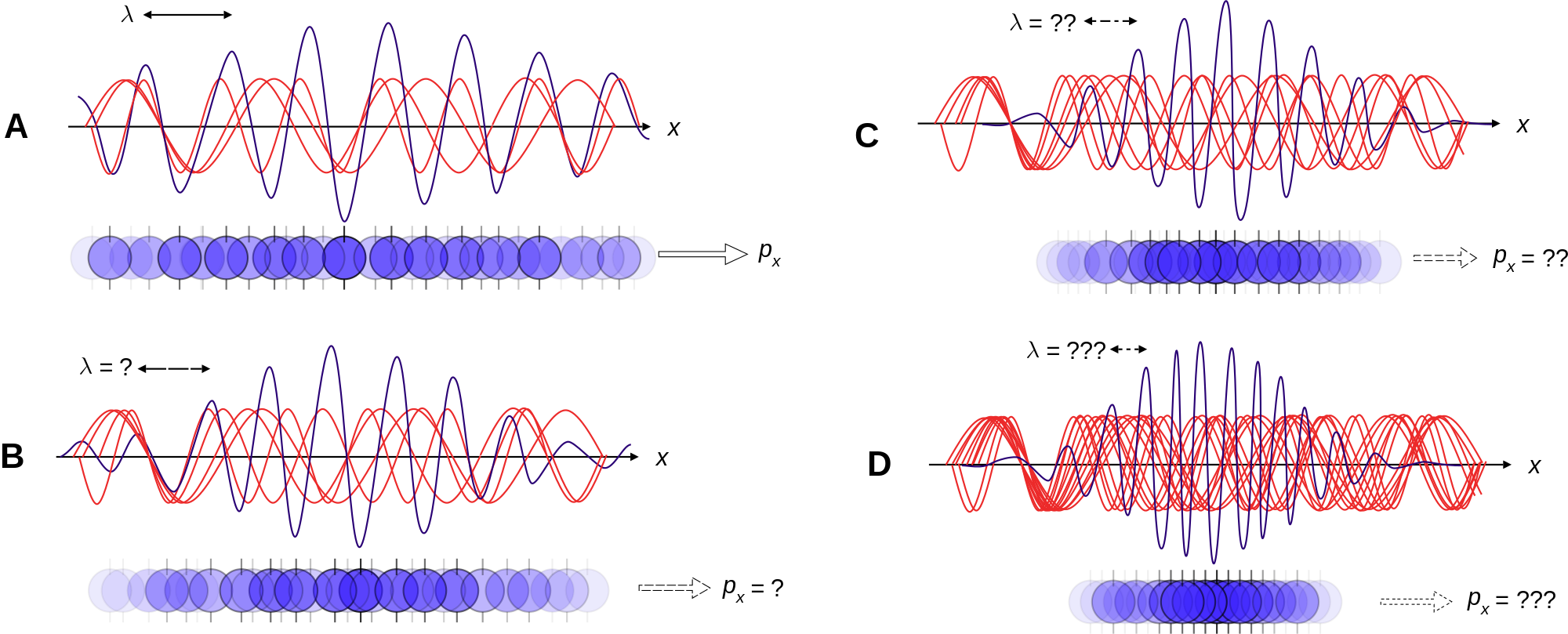
Ayrıca 1927’de Heisenberg kuantum fiziğine büyük bir katkı daha yaptı. Belirsizlik ilkesi olarak tanımlanan ilke, 1927 yılında Werner Heisenberg tarafından öne sürüldü.

Kuantum fiziğinde Heisenberg’in belirsizlik ilkesine göre, bir parçacığın momentumu ve konumu aynı anda tam doğrulukla ölçülemez (momentum değişimi = kütle değişimi x hız değişimi). Belirsizlik ilkesini daha da genellenmiş olarak anlatmak istersek şunları söyleyebiliriz. Kökleşik (klasik, deterministik) fizikten ayrı olarak kuantum fiziğinde her fiziksel niceliğe denk gelen bir gerçek sayı değil, bir işlemci vardır. Bu işlemciler, kökleşik mekanikten ayrı olarak sayısal değerler ile değil matrisler ile temsil edilir. Dolayısıyla, kuantum mekaniğinde ölçülen fiziksel niceliğin ölçüm sırası önemlidir. Herhangi iki fiziksel niceliği (örneğin: konum ve momentum) ele alalım. Eğer bu fiziksel niceliklere denk gelen iki işlemci yer değiştiremiyorsa bu iki niceliğin (örneğin: momentum ve konum) aynı anda ölçülmesi olanaksızdır. Bu durumda kesin sonuçlardan değil, bir ortalama değer yakınlarında dalgalanan değerlerden söz edebiliriz.

Belirsizlik ilkesi günlük boyutlu nesneler için de geçerlidir, ancak fark edilmez çünkü hassasiyet eksikliği olağanüstü küçüktür. Morningside College’dan (Sioux City, IA) Dave Slaven’a göre, bir beyzbolun hızının 0,1 mil / saat’lik bir hassasiyet içinde olduğu biliniyorsa, topun konumunu bilmek için mümkün olan maksimum hassasiyet 0.000000000000000000000000000008 milimetredir.

Kaynakça

1. Encyclopedia Britannica – Quantum Mechanics
2. Quantum Mechanical Model by Nuffield Foundation
3. Matter as a Wave