Kuantum dolanıklık alışık olmayanlar için karışık görünen ve üzerine yazılmış pek çok popüler yazı bulunabilecek bir konu. Ne yazık ki bazen fazla mistifiye edilmesi ve garip anlamlar yüklenmesi nedeniyle insanlarda, sanki anlaması zor bir kavram olduğu fikrini uyandırmakta. Bu yazıda kuantum dolanıklık fenomenini kullanarak herhangi iki nokta arasında, en azından kuramsal düzeyde, yüzde yüz güvenli iletişim kurma fikrinin temellerine değineceğiz.
Şifreli İletişim
Eldeki yazı içinde kriptolojinin temellerine ve türlerine girmeyeceğiz, bunlar için sitemizde daha önce üzerine yazdığımız “Şifrelerin Matematiği: Kriptografi” ve/veya “Kriptografiye Giriş: Şifreleme Teorisi” isimli kitaplara göz atabilirsiniz. Bunun yerine olabildiğince basit örnekler üzerinden bir anlatı kurmayı tercih edeceğiz.
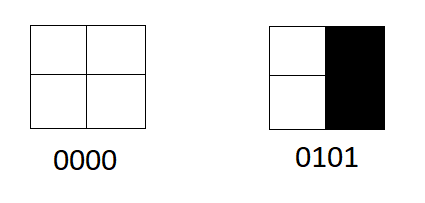
Yukarıda iki tane ikiye ikilik, toplam dört kareden oluşan bir mesaj var. Eğer bu mesaj size dördü de beyaz gelirse 0000, sağdaki gibi gelirse de 0101 olarak kodlandığını düşünelim. Yani beyaz kareler 0, siyah kareler 1 demek. Toplamda 4 bit veriden oluşan bu resmin 2 üzeri 4 hesabından 0000, 0001… 1110, 1111’e kadar uzanan 16 farklı şekilde bulunabileceğini biliyoruz (2x2x2x2 = 16).
Karelerde toplama işlemini de ikili kurallara göre yukarıdaki gibi yapabileceğimizi düşünelim. Yani 01 + 01 = 10 edecek şekilde, burada ikili sistem kullandığımız için 2 rakamı 10, 3 rakamı 11, 4 rakamı 100 şeklinde yazılabiliyor. Dolayısıyla 1111 aslında 1000 + 0100 + 0010 + 0001, yani 8 + 4 + 2 + 1 = 15 ediyor, 0000 = 0 olarak başladığımız için de yukarıdaki şekil üzerindeki boyalı kareler üyeleri {0,1,2…,14,15} olan 16 elemanlı bir kümeye tekabül ediyor.
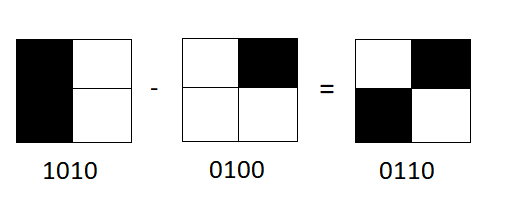
Eğer ben size 1010 mesajını gönderip anahtarımın da 0100 olduğunu söylemiş olsaydım size aslında göndermeye çalıştığım mesajın 0110 olduğunu anlayabilirdiniz. Ancak size yalnızca 1010 mesajını gönderip bunun şifreli bir mesaj olduğunu söyleseydim, 0000 ila 1111 arasındaki 16 olasılıktan herhangi birisini anahtar olarak kullanmış olabileceğimden ötürü elinizde 16 farklı ihtimali olan bir mesaj olurdu. [Burada ufak bir not olarak 1111 + 0001 = 10000 olduğunu ancak elimizde yalnızca dört kare olduğundan bunun size 0000 olarak görüneceğini hatırlatalım, aşağıdaki resim daha açıklayıcı olabilir.]
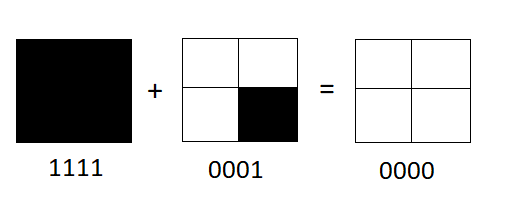
Kuantum Bunun Neresinde?
Şimdiye kadar yalnızca kare boyayarak gösterdiğimiz hikayenin kuantum mekaniğiyle hiçbir ilgisi yok, yaptığımız her şey sadece toplama ve çıkarma. Aynı anahtarı iki tarafın da şifreleme ve çözme işlemi için kullandığı sisteme kısaca “simetrik anahtarlı şifreleme” diyebiliriz, mesajı şifreleyen de çözen de aynı anahtar (aksi durumlar için kitaplara bakabilirsiniz). Mesajla aynı uzunlukta bir simetrik anahtarın yalnızca tek seferlik kullanıldığı durumlara ise ‘tek kullanımlık şerit’ (one-time-pad) anahtarlar deniyor, yani anahtarınızı yalnızca kendisiyle aynı boydaki bir mesajı şifrelemek ve çözmek için tek seferlik kullanıyorsunuz.
Alternatif olarak iki haneli bir anahtar da kullanabilirdiniz, örneğin 10’ı anahtar olarak seçmiş olsaydınız 0101 mesajını şifrelemek için iki kere 10’i tekrarlayıp 1010’ı anahtar yapabilirdiniz. Ancak bu tek kullanımlık şerit kadar güvenli olmazdı zira 16 değil yalnızca 8 olası anahtarınız olurdu (örneğin asla 0110 gibi bir anahtar üretemezdiniz). Bu da anahtarınızın boyutunu bilen bir şifre kırıcının işini yarı yarıya kolaylaştırırdı.
Tek kullanımlık şerit şifreleme dünyasında kırılamayacağı garantilenmiş bir şifreleme metodu, örneğin yalnızca 32 bit veri içeren (yani 4 byte) bir mesaj için 4,294,967,296 potansiyel anahtar olabilir. Ortalama bir MMS mesajının bile 600 kilobyte, yani 600 x 1000 x 8 = 4800000 bit veri içerdiğini göz önünde bulundurursak potansiyel anahtar sayısının saçma bir sayı olduğunu görebiliriz (4800000 tane 2’yi birbiriyle çarpın). Peki neden sürekli bunu kullanmıyoruz sorusunun yanıtıysa bir o kadar komik, anahtarı güvenli dağıtabilecek yöntemimiz yok!
Bazı büyük ve güvenliğe önem veren firmalar bu tek kullanımlık şeritleri fiziksel olarak birkaç terabyte’lık (yaklaşık 8,000,000,000,000 bit) harddisklere yükleyip bazen kıtalar arası güvenilir kuryeler aracılığıyla taşıma yoluyla bunu gerçekleştiriyorlar, ancak bunun fazlasıyla maliyetli olduğu açık. Üstüne üstlük kuryeye (veya çalıştığınız firmaya) güvenmenizi gerektiriyor. İşte kuantum dolanıklık burada devreye giriyor.
Kuantum Dolanık Durumlar
Yukarıdaki özel kuantum durumlarına alanın en büyük isimlerinden olan John Stewart Bell’in anısına Bell durumları deniyor. Bunlar olası iki durumu olan (0 ve 1) iki parçacığın maksimum dolanık durumda olabildiği muhtemel dört senaryoyu gösteriyor.
Örneğin ilk durumu ele alalım, 00 + 11. Baştaki bir bölü kök iki bize 00’ın da 11’inde ihtimalinin %50-%50 olduğunu gösteriyor. Yani bizim elimizde bu kuantum durumu olsa ve ölçüm yaparsak %50 ihtimalle 00 veya %50 ihtimalle 11 göreceğiz demek. Peki ya bu durum bir kişinin değil de iki kişinin eline dağıtılmış olsa?
İlk Bell durumundan (00+11) elinizde olduğunu düşünün ve bundaki parçacıkları iletişim kurmak istediğiniz bir arkadaşınızla paylaştınız. Sadece sizin elinizde olan (yani ilk parçacık) sizin bakış açınızdan aşağıdaki durumda olacaktır.
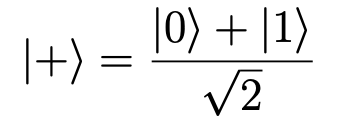
Arkadaşınız kendi parçacığına (ikinci parçacığa) baktığında o da yukarıdaki durumun aynısını görecektir. Dolayısıyla ikiniz de, eğer kendi parçacığınızı diğerini göz ardı ederek ölçerseniz %50 ihtimalle 0, %50 ihtimalle 1 bulacaksınız. Ancak kuantum dolanıklık işte tam bu noktada devreye giriyor. Belki fark etmişsinizdir, eğer sizin elinizde + varsa ve arkadaşınızın da elinde + varsa ortak durum aslında ++ durumu demektir. Bu da aşağıdaki kuantum duruma tekabül eder.
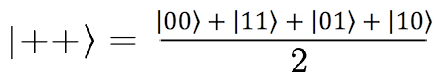
Bu durum görebileceğiniz üzere başta elimizde olduğunu iddia ettiğimiz Bell durumu değil. Dolayısıyla, kendi parçacığımıza ve arkadaşımızın parçacığına ayrı ayrı bakarak yaptığımız çıkarım yanlış! Doğrusunu görebilmek için ikisine aynı anda bakabilmemiz gerekiyor. İşte bu özellik, klasik mekanikte karşılığı olmayan ve kuantum mekaniksel parçacıklara özgü bir davranış, parçacıkların arasında yerel olmayan korelasyonların var olması.
Klasik mekanikte her parçacık kendi özelinde ele alınıp sonra sistem tüm bu parçacıkların toplamı olarak ortaya konulur, ancak kuantum mekaniğinde sistemin kendisi parçalarının toplamından ‘farklı’ bir bilgi içerebilir, yalnızca kendi elinizdeki parçacığa bakarak erişemeyeceğiniz bir bilgi. Kuantum mekaniğinde bütün, teker teker parçalarının toplamından daha çok bilgi içerebilir.
Şimdi elimizde aşağıdaki gibi bir anahtar olduğunu ve bunu arkadaşınızla aranızda paylaştığınızı varsayalım.
Sizin elinizdeki anahtar 16’da 1 ihtimalle her olasılık (0000, 0001, 0010,… ,1111) gelebilir, arkadaşınızın elindeki anahtar da 16’da 1 ihtimalle her olasılık (0000, 0001, 0010,… ,1111) gelebilir. Ancak sonradan kontrol edecek olursanız size 0100 geldiyse mutlaka arkadaşınıza da 0100 geldiğini göreceksiniz! Çünkü yukarıdan da hatırlayacağınız üzere, her bir basamak için Bell durumları ya 00 ya 11 olmak zorunda, siz 0 gördüyseniz arkadaşınız da mutlaka sıfır görmüş olacak.
Eğer verili bir mesajı siz elinizdeki birinci parçacığı kullanarak şifrelerseniz arkadaşınız da kendi elindeki ikinci parçacığı kullanarak çözebilir, aslında kuramsal olarak aradaki anahtarı sizin dahi bilmenize gerek kalmaz. Fakat bilmeniz gereken durumlarda bile hiç kimse araya girip sizi dinleyemez, araya birisi girip arkadaşınızla aranızdaki dolanıklığa eklemlenmeye çalışırsa başarısız olacaktır çünkü maksimum dolanıklık ancak iki parçacık arasında olabilir (buna dolanıklığın tek eşliliği adı verilir). Aranıza girmeye çalışan kişi kuantum dolanıklık durumunu bozmuş olacağından artık anahtarlarınız simetrik olmayacaktır, bu nedenle de şifre çözme işinde işlevini yitirecektir.
Dolanıklık Elde Etme
Peki bu özel dolanık durumları nasıl elde edebiliriz diye sorabilirsiniz. Daha önce yazdığımız “Kuantum Bilgisayarların Matematiği Üzerine” yazısını okuyanlar yukarıdaki kuantum durumlarında tanıdık işaretler görmüş olabilir. Kullanmayı tercih ettiğimiz birinci Bell durumunu kuantum mantık kapılarını kullanarak elde edilişini aşağıdaki şekilde görebilirsiniz.
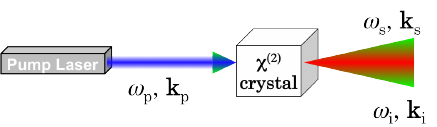
Yani bir Hadamard ve bir C-NOT kapısıyla bu kuantum durumunu elde edebiliriz. Ancak kuantum mantık kapılarını kullanmadan, fiziksel başka yöntemlerle de dolanık parçacıklar elde etmek mümkün. Örneğin aşağıda, bir kaynak lazeri özel bir kristal türünden geçirerek enerjisi düşürülmüş ancak birbiriyle dolanık hale sokulmuş iki ışık huzmesi elde etmeyi gösteren bir mekanizma görülebilir (bu yönteme ‘spontaneous parametric down conversion’ / ‘kendiliğinden parametrik aşağı çevrim’ denir).
Şeytan Bunun Neresinde
Şimdiye kadar her şey kulağa kuantum dolanıklık bazlı iletişim güvenlik problemimize mucizevi bir çözümmüş gibi geliyor, o zaman neden hala bu sisteme geçmedik?
İlk baştaki dört kareden oluşan resimlerimizi hatırlayın, aslında onlar bir nevi küçük kare kodlar olarak düşünülebilir. QR kodlar versiyonlarına bağlı olarak farklı miktarlarda veri barındırabilirler, ancak düz düşünecek olursak yukarıda 30×30’dan 900 kare bulunmakta, bu da 900 tane Bell durumu demek, basit bir qr kodu için.
Peki şimdi bunu arkadaşınızla yaptığınız öylesine bir WhatsApp konuşması temelinde, paylaştığınız emojileri ve mesaj kalabalığını göz önüne alarak hayal edin. Veya milyonlarca insanın su, elektrik, doğalgaz faturası ödemesinden kaynaklanan ‘gündelik’ bankacılık işlemlerinin hacmini. Bu kadar verinin hepsinin kuantum şifrelemeyle güvenli hale getirilmesinin neredeyse imkansız olduğu aşikar.
Daha önce “Tüm Sırların İfşa Olacağı Gün Yaklaşırken” başlıklı yazımızda kuantum bilgisayarların Shor algoritmasını kullanarak internetin şifreleme altyapısı olan RSA yöntemini kıracağından bahsetmiştik. Belki kuantum bilgisayarlara gerek bile kalmadan, çok daha gelişmiş klasik bir algoritma bile bunu yapabilir (yapılamayacağının matematiksel kanıtı yok). Bir başka yazımızdaysa “Hassas Verilerin Korunması Neden Önemlidir” sorusuna odaklanmıştık. Uzun vadede değeri olan verilerin (sağlık verileri gibi) olabildiğince erkenden kuantum-sonrası (post-quantum) kriptografik yöntemlerle korunmaya başlanmasının önemine değinmiş, olası bir senaryo üzerinden böylesi verilerin kaybedilmesinin uzun vadede ülkelere verebileceği zararlara dair küçük bir örnek vermiştik.
Toparlarsak
Bu yazıda kısaca kuantum dolanık parçacıklarla simetrik anahtar yaratımı üzerine bir genel tema aktarmaya çalıştık. Alanın geçmişine baktığımızda iki protokolün tüm bu süreci başlattığını söylemek mümkün, BB84 ve E91. BB84 yalnızca süperpozisyonu, E91 ise dolanıklığı kullanan protokoller. Bunların üzerine yazılmış Türkçe eserler dağınık da olsa bulunmakta (bir örnek). Konuyla ilgili güzel genel bir özet içinse Kutlu Kutluer’in Twitter paylaşımlarına bakılabilir.
Kuantum bilgisayarlar ilgi çekici ve heyecan uyandırıcı olabilirler, ancak kuantum kriptografi çoktandır burada olan ve ticari olarak aktif bir alan. Üstüne üstlük bu alandaki bilgi ve tecrübeler ileride kurulacak her türlü kuantum endüstrisine de aktarılabilir. Kuantum bilgisayım için kuantum kriptografinin neden önemli olduğuna dair geçtiğimiz ay PBS Space Time’ın hazırladığı bir giriş videosuna aşağıdan ulaşabilirsiniz.
Sonuç olarak kabul etmek gerekiyor ki, kuantum teknolojileri çok geniş bir spektrumdan gelecek. Bunlara şimdiden hazırlanmak ve genel kuantum fenomenlerinin (süperpozisyon, dolanıklık, bağlamsallık, belirsizlik ilkesi gibi gibi) teknolojiyle nerelerde bağlandığını görmek önemli. Gelecek herkesin beklediğinden hızlı geliyor olabilir.
Bu içerik orijinal olarak Düzensiz.org üzerinde yayınlanmıştır.
справки
What’s up, yes this piece of writing is in fact nice and I have learned lot of things from it about blogging. thanks.
It’s remarkable to go to see this web site and reading the views of all friends about this article, while I am also keen of getting familiarity.
Way cool! Some very valid points! I appreciate you writing this article and the rest of the site is also really good.
hey there and thank you for your information I’ve definitely picked up anything new from right here. I did however expertise some technical issues using this site, since I experienced to reload the web site many times previous to I could get it to load properly. I had been wondering if your hosting is OK? Not that I am complaining, but sluggish loading instances times will very frequently affect your placement in google and can damage your quality score if advertising and marketing with Adwords. Anyway I’m adding this RSS to my e-mail and can look out for a lot more of your respective interesting content. Make sure you update this again soon.
Keep this going please, great job!
Heya i’m for the first time here. I came across this board and I find It truly useful & it helped me out a lot. I hope to give something back and help others like you helped me.
Do you mind if I quote a couple of your posts as long as I provide credit and sources back to your weblog? My website is in the very same area of interest as yours and my visitors would definitely benefit from a lot of the information you present here. Please let me know if this okay with you. Cheers!
wonderful post, very informative. I wonder why the other experts of this sector do not realize this. You should continue your writing. I am sure, you have a huge readers’ base already!
Good day very nice web site!! Guy .. Beautiful .. Superb .. I will bookmark your website and take the feeds also? I am satisfied to seek out so many useful information here in the publish, we’d like develop more strategies in this regard, thank you for sharing. . . . . .
Good answer back in return of this issue with real arguments and explaining all about that.
Hi, i feel that i saw you visited my website so i got here to go back the favor?.I am trying to find things to improve my website!I guess its ok to use some of your ideas!!
Whats up very nice web site!! Guy .. Beautiful .. Amazing .. I will bookmark your website and take the feeds also? I am satisfied to seek out so many useful information here in the post, we need develop more strategies in this regard, thank you for sharing. . . . . .
Thank you for some other informative blog. Where else may I am getting that kind of info written in such a perfect means? I have a undertaking that I am simply now running on, and I have been at the glance out for such information.
Nice post. I learn something new and challenging on sites I stumbleupon everyday. It will always be interesting to read content from other writers and practice a little something from their sites.
I visit everyday some web pages and information sites to read articles, but this weblog offers quality based articles.
What’s up, its good post about media print, we all understand media is a impressive source of information.
Hello there, simply became aware of your blog thru Google, and found that it is really informative. I’m gonna watch out for brussels. I will appreciate for those who continue this in future. Lots of other people will probably be benefited from your writing. Cheers!
Hello there! Do you know if they make any plugins to help with SEO? I’m trying to get my blog to rank for some targeted keywords but I’m not seeing very good gains. If you know of any please share. Kudos!
First off I want to say wonderful blog! I had a quick question that I’d like to ask if you don’t mind. I was curious to know how you center yourself and clear your thoughts before writing. I have had a hard time clearing my mind in getting my thoughts out. I do enjoy writing but it just seems like the first 10 to 15 minutes are wasted just trying to figure out how to begin. Any suggestions or tips? Cheers!
Hey! Do you use Twitter? I’d like to follow you if that would be ok. I’m undoubtedly enjoying your blog and look forward to new updates.
Wow, that’s what I was looking for, what a data! present here at this webpage, thanks admin of this website.
Hurrah! Finally I got a webpage from where I can really get helpful data regarding my study and knowledge.
When someone writes an piece of writing he/she maintains the idea of a user in his/her mind that how a user can understand it. So that’s why this article is great. Thanks!
I like the valuable information you supply in your articles. I will bookmark your weblog and check again here frequently. I am rather certain I will be told many new stuff right here! Good luck for the following!
Hello just wanted to give you a brief heads up and let you know a few of the pictures aren’t loading properly. I’m not sure why but I think its a linking issue. I’ve tried it in two different web browsers and both show the same outcome.
I think one of your adverts triggered my browser to resize, you might want to put that on your blacklist.
Normally I do not learn article on blogs, but I would like to say that this write-up very pressured me to take a look at and do so! Your writing style has been surprised me. Thank you, quite nice post.
Nice blog here! Also your website loads up fast! What host are you using? Can I get your affiliate link to your host? I wish my website loaded up as fast as yours lol
Wow, that’s what I was seeking for, what a data! present here at this webpage, thanks admin of this web site.
I’m impressed, I must say. Rarely do I encounter a blog that’s both educative and engaging, and let me tell you, you have hit the nail on the head. The issue is something not enough people are speaking intelligently about. I am very happy that I stumbled across this in my search for something concerning this.
Most of what you say is astonishingly appropriate and it makes me wonder the reason why I had not looked at this with this light previously. This article really did turn the light on for me as far as this specific subject matter goes. Nevertheless at this time there is actually just one factor I am not necessarily too comfy with so whilst I try to reconcile that with the central theme of your point, permit me observe what all the rest of your readers have to point out.Very well done.
Thanks to my father who informed me concerning this webpage, this blog is really awesome.
Hi there, yes this piece of writing is really good and I have learned lot of things from it regarding blogging. thanks.
Hi there to all, the contents present at this website are actually remarkable for people experience, well, keep up the nice work fellows.
Wow! I’m in awe of the author’s writing skills and capability to convey complex concepts in a straightforward and clear manner. This article is a real treasure that merits all the accolades it can get. Thank you so much, author, for sharing your expertise and offering us with such a precious resource. I’m truly appreciative!
I am not sure where you are getting your information, but great topic. I needs to spend some time learning much more or understanding more. Thanks for magnificent information I was looking for this info for my mission.
Thanks for your write-up on this weblog. From my experience, often times softening upward a photograph could provide the digital photographer with an amount of an inspired flare. Oftentimes however, this soft clouds isn’t just what you had planned and can often times spoil an otherwise good photograph, especially if you anticipate enlarging the item.
Wow that was strange. I just wrote an very long comment but after I clicked submit my comment didn’t show up. Grrrr… well I’m not writing all that over again. Anyway, just wanted to say superb blog!
Have you ever considered about including a little bit more than just your articles? I mean, what you say is valuable and all. Nevertheless think about if you added some great graphics or video clips to give your posts more, “pop”! Your content is excellent but with images and video clips, this website could undeniably be one of the very best in its niche. Good blog!
I have observed that service fees for online degree professionals tend to be an awesome value. For instance a full 4-year college Degree in Communication from The University of Phoenix Online consists of 60 credits at $515/credit or $30,900. Also American Intercontinental University Online makes available Bachelors of Business Administration with a entire education course feature of 180 units and a price of $30,560. Online learning has made obtaining your certification far more easy because you may earn your own degree through the comfort in your home and when you finish from office. Thanks for all your other tips I have certainly learned through the web site.
Great paintings! This is the kind of info that are meant to be shared around the net. Shame on the seek engines for no longer positioning this publish higher! Come on over and discuss with my site . Thank you =)
fantastic submit, very informative. I wonder why the other experts of this sector don’t notice this. You should proceed your writing. I’m sure, you have a great readers’ base already!
I was pretty pleased to find this great site. I wanted to thank you for your time just for this wonderful read!! I definitely loved every little bit of it and I have you book-marked to check out new stuff on your website.
Unquestionably believe that that you stated. Your favourite justification appeared to be at the net the simplest thing to bear in mind of. I say to you, I definitely get irked whilst other folks consider worries that they plainly do not realize about. You controlled to hit the nail upon the top as smartly as defined out the whole thing with no need side effect , other people can take a signal. Will likely be back to get more. Thank you
This is very interesting, You are a very skilled blogger. I have joined your feed and look forward to seeking more of your great post. Also, I have shared your site in my social networks!
Excellent blog here! Also your site lots up fast! What host are you using? Can I am getting your associate link on your host? I desire my site loaded up as fast as yours lol
Aw, this was a very nice post. In concept I wish to put in writing like this moreover ? taking time and actual effort to make an excellent article? however what can I say? I procrastinate alot and in no way appear to get one thing done.
Someone essentially help to make seriously articles I would state. This is the first time I frequented your website page and thus far? I surprised with the research you made to create this particular publish amazing. Great job!
Way cool! Some very valid points! I appreciate you writing this article and the rest of the site is extremely good.
I?ll immediately grab your rss as I can not find your e-mail subscription link or e-newsletter service. Do you have any? Kindly let me know in order that I could subscribe. Thanks.
Woah! I’m really enjoying the template/theme of this website. It’s simple, yet effective. A lot of times it’s difficult to get that “perfect balance” between superb usability and visual appeal. I must say you have done a superb job with this. In addition, the blog loads extremely fast for me on Opera. Superb Blog!
Wonderful beat ! I would like to apprentice while you amend your website, how can i subscribe for a blog site? The account aided me a acceptable deal. I had been a little bit acquainted of this your broadcast offered bright clear idea
First off I want to say wonderful blog! I had a quick question that I’d like to ask if you don’t mind. I was curious to know how you center yourself and clear your thoughts before writing. I have had a hard time clearing my mind in getting my thoughts out. I do enjoy writing but it just seems like the first 10 to 15 minutes are usually wasted just trying to figure out how to begin. Any suggestions or tips? Appreciate it!
Hi, I think your blog might be having browser compatibility issues. When I look at your blog in Safari, it looks fine but when opening in Internet Explorer, it has some overlapping. I just wanted to give you a quick heads up! Other then that, fantastic blog!
Исключительный частный эротический массаж Москва база массажа
You can definitely see your skills within the paintings you write. The sector hopes for more passionate writers like you who are not afraid to say how they believe. Always follow your heart.
Hello there, just became aware of your blog through Google, and found that it is really informative. I’m gonna watch out for brussels. I will appreciate if you continue this in future. A lot of people will be benefited from your writing. Cheers!
I have been browsing on-line more than three hours as of late, but I never discovered any fascinating article like yours. It is lovely value enough for me. In my opinion, if all web owners and bloggers made excellent content material as you did, the net can be much more useful than ever before.
Have you ever thought about adding a little bit more than just your articles? I mean, what you say is fundamental and all. Nevertheless think about if you added some great photos or video clips to give your posts more, “pop”! Your content is excellent but with images and video clips, this website could definitely be one of the best in its niche. Amazing blog!
Hurrah! Finally I got a webpage from where I know how to in fact take useful data regarding my study and knowledge.
It’s going to be end of mine day, except before finish I am reading this impressive piece of writing to increase my experience.
I believe one of your advertisings caused my internet browser to resize, you may well want to put that on your blacklist.
I have noticed that online diploma is getting common because attaining your college degree online has changed into a popular alternative for many people. Quite a few people have certainly not had a possibility to attend an established college or university yet seek the improved earning possibilities and career advancement that a Bachelors Degree grants. Still other individuals might have a diploma in one field but would like to pursue another thing they now possess an interest in.
This excellent website really has all of the info I wanted about this subject and didn’t know who to ask.
It’s very trouble-free to find out any topic on net as compared to books, as I found this piece of writing at this website.
I really believe that a property foreclosure can have a important effect on the client’s life. House foreclosures can have a Seven to ten years negative influence on a client’s credit report. A borrower who have applied for a home loan or just about any loans for that matter, knows that your worse credit rating will be, the more hard it is to obtain a decent loan. In addition, it might affect the borrower’s chance to find a respectable place to lease or hire, if that turns into the alternative housing solution. Interesting blog post.
Oh my goodness! an incredible article dude. Thanks However I am experiencing situation with ur rss . Don?t know why Unable to subscribe to it. Is there anybody getting an identical rss drawback? Anybody who is aware of kindly respond. Thnkx
Good day! I know this is somewhat off topic but I was wondering if you knew where I could get a captcha plugin for my comment form? I’m using the same blog platform as yours and I’m having difficulty finding one? Thanks a lot!
Thank you for some other informative web site. Where else may just I am getting that kind of info written in such a perfect means? I have a undertaking that I am simply now operating on, and I have been at the glance out for such information.
Ahaa, its good discussion about this piece of writing here at this blog, I have read all that, so now me also commenting here.
Wonderful blog! Do you have any tips for aspiring writers? I’m planning to start my own site soon but I’m a little lost on everything. Would you suggest starting with a free platform like WordPress or go for a paid option? There are so many options out there that I’m totally confused .. Any ideas? Thanks!
Undeniably believe that which you stated. Your favorite justification appeared to be on the net the simplest thing to be aware of. I say to you, I definitely get irked while people consider worries that they plainly do not know about. You managed to hit the nail upon the top as well as defined out the whole thing without having side effect , people can take a signal. Will likely be back to get more. Thanks
After research a number of of the weblog posts on your web site now, and I really like your method of blogging. I bookmarked it to my bookmark web site list and might be checking back soon. Pls try my website as nicely and let me know what you think.
Woah! I’m really digging the template/theme of this site. It’s simple, yet effective. A lot of times it’s tough to get that “perfect balance” between user friendliness and visual appeal. I must say you’ve done a amazing job with this. Also, the blog loads very quick for me on Opera. Exceptional Blog!
Hey there! This is my first visit to your blog! We are a collection of volunteers and starting a new initiative in a community in the same niche. Your blog provided us valuable information to work on. You have done a marvellous job!
Hmm is anyone else having problems with the images on this blog loading? I’m trying to figure out if its a problem on my end or if it’s the blog. Any feed-back would be greatly appreciated.
Normally I do not read article on blogs, however I wish to say that this write-up very pressured me to try and do so! Your writing taste has been amazed me. Thank you, quite great article.
Good answer back in return of this question with solid arguments and describing all about that.
Hello There. I found your blog using msn. This is an extremely well written article. I?ll be sure to bookmark it and come back to read more of your useful info. Thanks for the post. I?ll certainly comeback.
Also a thing to mention is that an online business administration diploma is designed for scholars to be able to easily proceed to bachelor’s degree courses. The Ninety credit education meets the other bachelor diploma requirements and once you earn the associate of arts in BA online, you will possess access to up to date technologies with this field. Several reasons why students have to get their associate degree in business is because they are interested in the field and want to have the general education necessary ahead of jumping right into a bachelor education program. Many thanks for the tips you actually provide within your blog.
Hey There. I discovered your weblog the usage of msn. This is an extremely smartly written article. I will be sure to bookmark it and come back to read extra of your useful info. Thanks for the post. I?ll definitely comeback.
Wonderful beat ! I wish to apprentice whilst you amend your site, how can i subscribe for a weblog website? The account aided me a applicable deal. I were tiny bit familiar of this your broadcast provided bright transparent concept
Can I just say what a reduction to seek out somebody who really knows what theyre speaking about on the internet. You undoubtedly know the way to convey a problem to light and make it important. More folks need to read this and understand this facet of the story. I cant believe youre no more standard because you positively have the gift.
Thank you for this article. I would also like to talk about the fact that it can end up being hard when you find yourself in school and merely starting out to initiate a long credit history. There are many learners who are just trying to endure and have a lengthy or beneficial credit history can occasionally be a difficult thing to have.
It’s not my first time to pay a visit this site, i am visiting this site dailly and take nice information from here daily.
I love what you guys are usually up too. This sort of clever work and exposure! Keep up the great works guys I’ve incorporated you guys to our blogroll.
Great beat ! I would like to apprentice while you amend your site, how can i subscribe for a blog site? The account aided me a appropriate deal. I have been tiny bit familiar of this your broadcast provided vibrant transparent idea
Its like you read my mind! You appear to know a lot about this, like you wrote the book in it or something. I think that you could do with a few pics to drive the message home a bit, but instead of that, this is excellent blog. A great read. I’ll definitely be back.
An additional issue is that video games are generally serious anyway with the most important focus on learning rather than fun. Although, it comes with an entertainment part to keep children engaged, each one game is frequently designed to work towards a specific skill set or area, such as instructional math or scientific discipline. Thanks for your post.
Thanks for the a new challenge you have revealed in your article. One thing I’d prefer to reply to is that FSBO relationships are built as time passes. By presenting yourself to owners the first end of the week their FSBO can be announced, prior to a masses get started calling on Monday, you create a good interconnection. By sending them tools, educational components, free reviews, and forms, you become the ally. Through a personal affinity for them along with their predicament, you build a solid link that, on most occasions, pays off when the owners decide to go with an agent they know and also trust — preferably you actually.
I have been surfing online greater than three hours as of late, but I by no means found any attention-grabbing article like yours. It’s pretty value enough for me. Personally, if all webmasters and bloggers made excellent content as you probably did, the net will be a lot more useful than ever before.
F*ckin? awesome issues here. I am very satisfied to see your post. Thank you a lot and i am having a look ahead to touch you. Will you please drop me a e-mail?
Attractive part of content. I just stumbled upon your web site and in accession capital to assert that I acquire in fact enjoyed account your weblog posts. Anyway I?ll be subscribing in your augment and even I fulfillment you get entry to constantly quickly.
Admiring the time and effort you put into your blog and in depth information you offer. It’s nice to come across a blog every once in a while that isn’t the same out of date rehashed material. Excellent read! I’ve bookmarked your site and I’m including your RSS feeds to my Google account.
Nice post. I learn one thing more challenging on totally different blogs everyday. It can all the time be stimulating to learn content from other writers and apply just a little one thing from their store. I’d desire to make use of some with the content material on my weblog whether or not you don’t mind. Natually I’ll provide you with a link on your web blog. Thanks for sharing.
Heya i’m for the first time here. I came across this board and I find It truly useful & it helped me out a lot. I hope to give something back and help others like you helped me.
I will immediately grab your rss feed as I can not find your e-mail subscription link or newsletter service. Do you’ve any? Kindly let me know so that I could subscribe. Thanks.
I couldn’t resist commenting. Perfectly written!
Youre so cool! I dont suppose Ive learn something like this before. So nice to find any person with some unique thoughts on this subject. realy thank you for starting this up. this website is something that’s wanted on the web, someone with somewhat originality. useful job for bringing something new to the internet!
Hello there! I know this is kinda off topic but I was wondering if you knew where I could find a captcha plugin for my comment form? I’m using the same blog platform as yours and I’m having difficulty finding one? Thanks a lot!
Hey there I am so glad I found your blog page, I really found you by error, while I was searching on Askjeeve for something else, Regardless I am here now and would just like to say thanks a lot for a incredible post and a all round enjoyable blog (I also love the theme/design), I don’t have time to read through it all at the minute but I have book-marked it and also included your RSS feeds, so when I have time I will be back to read a great deal more, Please do keep up the fantastic job.
Greetings from Florida! I’m bored to tears at work so I decided to check out your site on my iphone during lunch break. I really like the info you present here and can’t wait to take a look when I get home. I’m amazed at how quick your blog loaded on my mobile .. I’m not even using WIFI, just 3G .. Anyhow, awesome site!
Does your website have a contact page? I’m having a tough time locating it but, I’d like to send you an e-mail. I’ve got some recommendations for your blog you might be interested in hearing. Either way, great website and I look forward to seeing it expand over time.
I’m so happy to read this. This is the kind of manual that needs to be given and not the accidental misinformation that is at the other blogs. Appreciate your sharing this greatest doc.
Howdy! I’m at work browsing your blog from my new iphone 3gs! Just wanted to say I love reading through your blog and look forward to all your posts! Carry on the excellent work!
Hi, I think your site might be having browser compatibility issues. When I look at your website in Safari, it looks fine but when opening in Internet Explorer, it has some overlapping. I just wanted to give you a quick heads up! Other then that, fantastic blog!
Thanks for the ideas you have discussed here. Furthermore, I believe there are many factors that will keep your insurance premium all the way down. One is, to bear in mind buying automobiles that are in the good directory of car insurance firms. Cars that are expensive tend to be at risk of being snatched. Aside from that insurance coverage is also depending on the value of your car or truck, so the higher in price it is, then higher this premium you make payment for.
Magnificent beat ! I wish to apprentice even as you amend your site, how can i subscribe for a blog web site? The account aided me a applicable deal. I were tiny bit familiar of this your broadcast provided vibrant transparent concept
You can definitely see your skills in the work you write. The world hopes for even more passionate writers like you who are not afraid to say how they believe. Always follow your heart.
I do accept as true with all the concepts you have introduced in your post. They are very convincing and will definitely work. Still, the posts are too quick for beginners. May you please extend them a bit from next time? Thank you for the post.
Mood changes can include euphoria and extreme depression and may alter the way
Heya i am for the first time here. I came across this board and I find It really useful & it helped me out much. I hope to give something back and aid others like you helped me.
Excellent website you have here but I was wanting to know if you knew of any discussion boards that cover the same topics talked about in this article? I’d really love to be a part of group where I can get opinions from other knowledgeable individuals that share the same interest. If you have any recommendations, please let me know. Many thanks!
I love reading through a post that will make people think. Also, thanks for allowing for me to comment!
Hmm it appears like your website ate my first comment (it was extremely long) so I guess I’ll just sum it up what I submitted and say, I’m thoroughly enjoying your blog. I as well am an aspiring blog blogger but I’m still new to the whole thing. Do you have any tips and hints for first-time blog writers? I’d certainly appreciate it.
Another thing I’ve noticed is always that for many people, poor credit is the reaction to circumstances past their control. One example is they may be actually saddled with illness so that they have large bills going to collections. It could be due to a work loss or even the inability to go to work. Sometimes breakup can truly send the money in an opposite direction. Many thanks sharing your ideas on this website.
Your positivity and enthusiasm are truly infectious! This article brightened my day and left me feeling inspired. Thank you for sharing your uplifting message and spreading positivity to your readers.
One thing is that one of the most common incentives for utilizing your credit cards is a cash-back or rebate supply. Generally, you will get 1-5 back upon various acquisitions. Depending on the credit card, you may get 1 back on most expenditures, and 5 again on buying made from convenience stores, filling stations, grocery stores and also ‘member merchants’.
Yet another thing I would like to talk about is that rather than trying to match all your online degree classes on days and nights that you complete work (since the majority people are fatigued when they go back home), try to get most of your sessions on the saturdays and sundays and only a few courses on weekdays, even if it means a little time off your saturdays. This is really good because on the week-ends, you will be much more rested and also concentrated with school work. Many thanks for the different recommendations I have discovered from your website.
This article is a true game-changer! Your practical tips and well-thought-out suggestions hold incredible value. I’m eagerly anticipating implementing them. Thank you not only for sharing your expertise but also for making it accessible and easy to apply.
Fantastic goods from you, man. I’ve understand your stuff previous to and you’re just too wonderful. I really like what you’ve acquired here, really like what you’re stating and the way in which you say it. You make it entertaining and you still take care of to keep it sensible. I cant wait to read far more from you. This is actually a great website.
Your writing style effortlessly draws me in, and I find it nearly impossible to stop reading until I’ve reached the end of your articles. Your ability to make complex subjects engaging is indeed a rare gift. Thank you for sharing your expertise!
Your positivity and enthusiasm are undeniably contagious! This article brightened my day and left me feeling inspired. Thank you for sharing your uplifting message and spreading positivity among your readers.
Great delivery. Great arguments. Keep up the good work.