Müzik dinlediğimizde kulağımız adeta bir hesaplama yapar: flütün tiz tınıları, kemanın orta perdeleri ve kontrabasın derin uğultusu, farklı frekanslarda ses dalgaları olarak havayı doldurur. Bu birleşik dalga kulak kanalından sarmal biçimli kokleaya ulaştığında, farklı uzunluktaki tüy hücreleri çeşitli frekanslarda rezonansa girerek karmaşık sinyali temel ses bileşenlerine ayırır.
Bu hesaplamayı matematiksel olarak modellemek ise ancak 19. yüzyılda mümkün oldu. 1800’lerin başında Fransız matematikçi Jean-Baptiste Joseph Fourier, herhangi bir fonksiyonu temel dalgalara ayırmanın yolunu keşfetti. Bu temel frekanslar yeniden birleştirildiğinde özgün fonksiyon geri elde edilebiliyordu. Günümüzde “Fourier dönüşümü” olarak adlandırılan bu teknik, Fransız Devrimi’nin ateşli bir savunucusu olan bu matematikçinin, matematikte de bir devrimi tetiklemesini sağladı.
Fourier dönüşümünün üzerine kurulu “harmonik analiz” adlı matematik dalı, fonksiyonların bileşenlerini inceler. Matematikçiler kısa sürede sayı teorisinden diferansiyel denklemlere, kuantum mekaniğine kadar pek çok alandaki derin bağlantıları ortaya çıkardılar. Günlük hayatımızda da dosya sıkıştırmadan ses sinyali iyileştirmeye kadar Fourier dönüşümünün izlerine rastlanır.
New York Üniversitesi ve Flatiron Enstitüsü’nden Leslie Greengard şöyle diyor: “Fourier analizinin matematikteki etkisini hafife almak zordur; matematik, fizik, kimya ve her alana dokunuyor.”
Tutku Ateşi
Fourier, 1768’de Devrim öncesi Fransa’da doğdu. On yaşında öksüz kaldı ve Auxerre’deki bir manastır okulunda yetişti. On yıl boyunca din mi yoksa matematik mi seçeceği konusunda kararsız kaldı; sonunda din eğitimini bırakıp öğretmenliğe yöneldi. 1794’te, Terör Dönemi sırasında, 26 yaşındayken—Fransa’daki devrimci çabalara destek vermiş olmasına rağmen—karşıdevrimci sayılan inançlarını dile getirdiği için tutuklandı ve hapsedildi. Giyotinle idam edilmek üzereydi.

Terör Dönemi, idamı gerçekleşmeden önce sona erdi ve Fourier 1795’te matematik öğretmenliğine geri döndü. Birkaç yıl sonra Napolyon Bonapart’ın bilimsel danışmanı olarak atandı ve Mısır işgali sırasında orduya katıldı. Mısır antikaları üzerine araştırmalar yürütürken, onu dönüşümünü geliştirmeye götürecek çalışmasına da orada başladı: ısı iletiminin matematiğini anlamak istiyordu. 1801’de Fransa’ya döndüğünde—Fransız ordusu Mısır’dan çıkarılmadan kısa süre önce çalınan Rosetta Taşı İngilizlere teslim edilmişti—Fourier’in aklında artık başka hiçbir şey yoktu.
Metal bir çubuğun bir ucunu ısıtırsanız, ısı çubuk tek bir sıcaklığa ulaşıncaya kadar yayılır. Fourier, çubuktaki ısı dağılımının basit dalgaların toplamı olarak ifade edilebileceğini öne sürdü. Çubuk soğudukça bu dalgalar enerji kaybeder; bu da genliklerinin azalmasına ve sonunda sönmelerine yol açar. Daha hızlı salınan—yani daha yüksek enerjili—bileşenler önce sönümlenir, ardından düşük frekanslılar gelir. Bu, pikolodan tubaya tüm çalgıların birer birer susarak sessizliğe karıştığı bir senfoniye benzer.
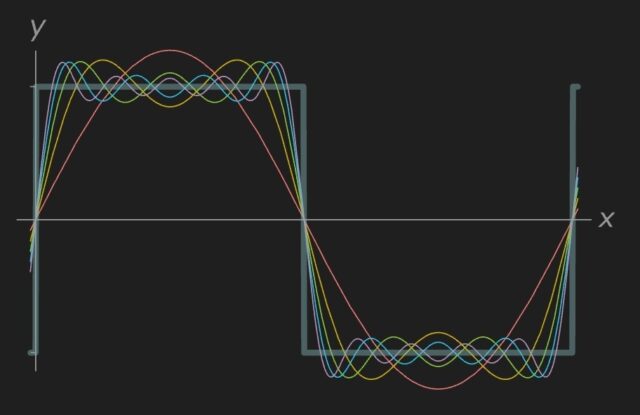
Öneri son derece radikaldi. Fourier, 1807’de Paris Enstitüsü’ndeki bir oturumda bu fikri sunduğunda, ünlü matematikçi Joseph-Louis Lagrange’ın çalışmasını “tam anlamıyla imkânsız” diye nitelediği aktarılır. Meslektaşlarını en çok rahatsız eden, ısı dağılımının kimi durumlarda son derece keskin ve düzensiz olabilmesiydi—örneğin bir çubuğun tam yarısının soğuk, diğer yarısının sıcak olduğu durum. Fourier, sıcaklıktaki bu ani sıçramanın matematiksel olarak temsil edilebileceğini savundu: Sonlu sayıda eğri yerine sonsuz sayıda daha basit eğrinin toplamı yeterliydi. Ne var ki dönemin çoğu matematikçisi, kaç tane düzgün eğriyi toplarsanız toplayın, keskin bir köşeye ulaşılamayacağına inanıyordu.
Bugün Fourier’in genel olarak haklı olduğunu biliyoruz.
Princeton Üniversitesi’nden matematikçi Charles Fefferman, “Herhangi bir şeyi bu çok, çok basit salınımların toplamı olarak temsil edebilirsiniz,” demişti. “Eğer elinizde bir sürü diyapazon varsa ve bunları mükemmel biçimde ayarlarsanız, Beethoven’ın Dokuzuncu Senfonisi’ni üretebileceğiniz biliniyor.” Bu süreç, yalnızca ne kadar yakınlaştırırsanız yakınlaştırın çılgınca salınan fonksiyonlar gibi en tuhaf örneklerde başarısız olur.
Peki Fourier dönüşümü nasıl çalışır?
İyi Eğitimli Bir Kulak
Fourier dönüşümü yapmak, bir parfümü koklayıp içindeki notaları (bileşenleri) ayırt etmeye ya da karmaşık bir caz akorunu dinleyip içindeki notaları seçmeye benzer.
Matematiksel olarak Fourier dönüşümü bir fonksiyondur: Girdi olarak, ilk bakışta karmaşık görünen bir fonksiyonu alır; çıktı olarak ise bir dizi frekans (ve bunlara karşılık gelen katsayılar) üretir. Bu frekanslardaki basit sinüs ve kosinüs dalgalarını—elde edilen katsayılarla—yazıp topladığınızda, özgün fonksiyonu yeniden elde edersiniz.
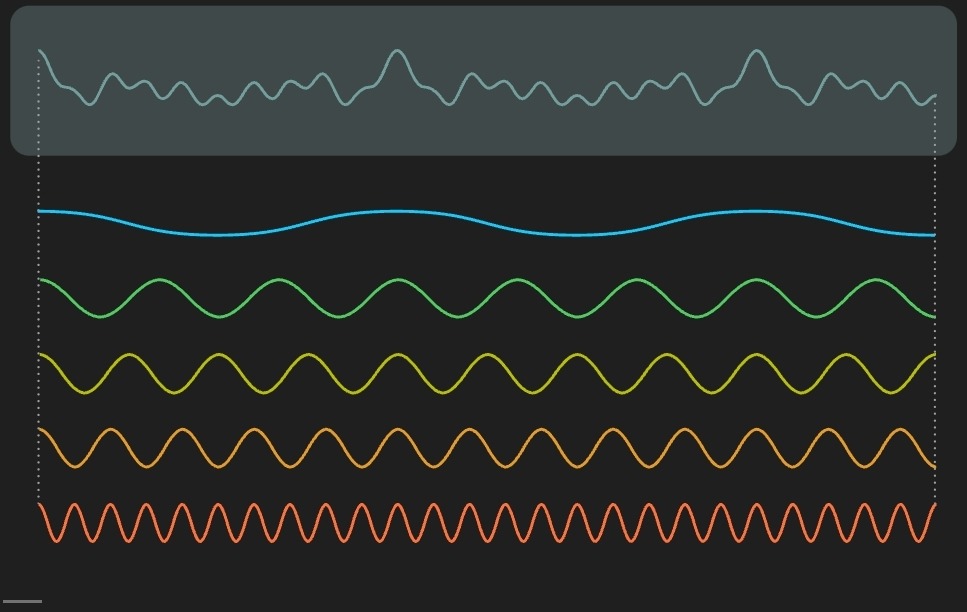
Bunu başarmak için Fourier dönüşümü, temelde tüm olası frekansları tarar ve her birinin özgün fonksiyona ne ölçüde katkı yaptığını belirler. Basit bir örnek olarak aşağıdaki fonksiyonu ele alalım:
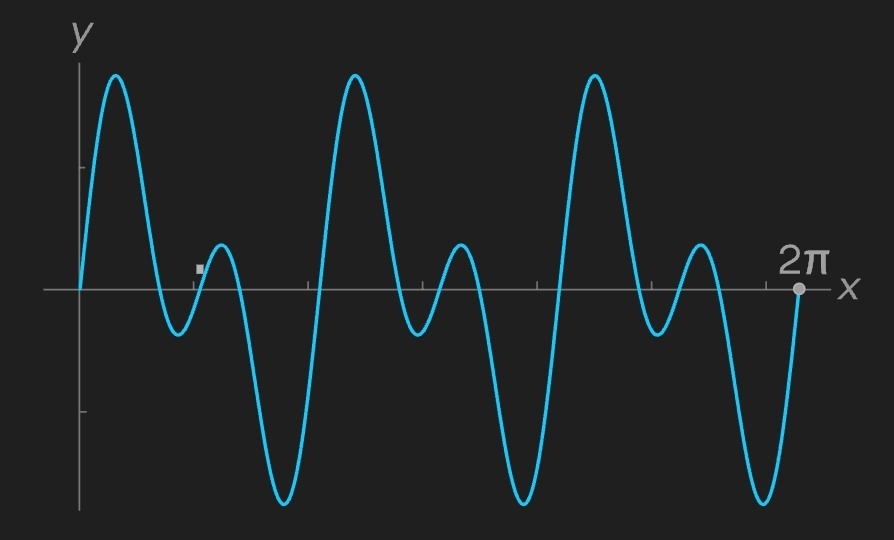
Fourier dönüşümü, her frekansın özgün fonksiyona ne kadar katkıda bulunduğunu ilgili dalgayla çarparak sınar. Örneğin, orijinali frekansı 3 olan bir sinüs dalgasıyla çarptığımızda şöyle bir sonuç elde ederiz:
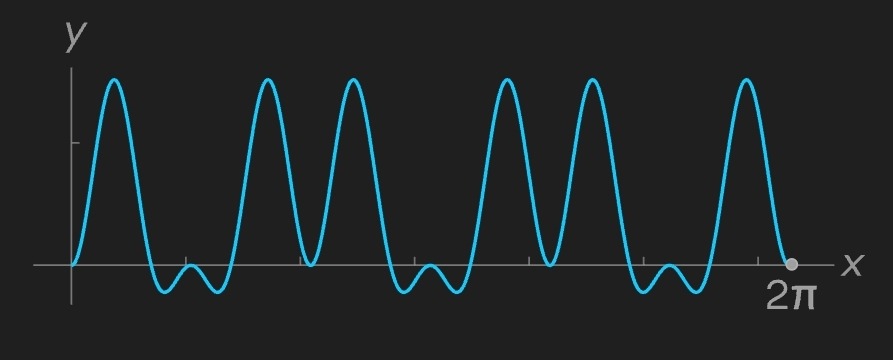
Çok sayıda büyük tepe noktası görülür; bu, 3 frekansının orijinale katkıda bulunduğunu gösterir. Tepe noktalarının ortalama yüksekliği, bu katkının büyüklüğünü yansıtır. Şimdi 5 frekansının mevcut olup olmadığını test edelim: orijinali frekansı 5 olan bir sinüsle çarptığımızda elde edeceğimiz sonuç şöyledir:
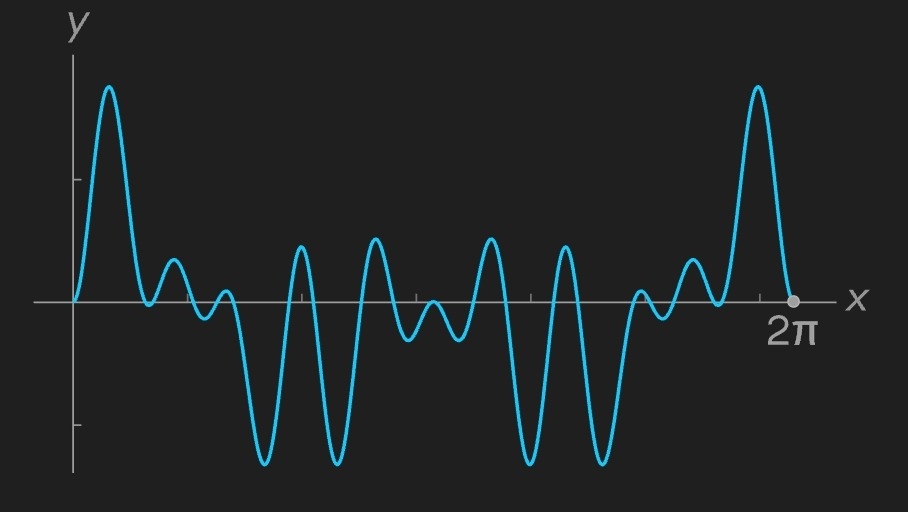
Bazı büyük tepe noktalarının yanı sıra belirgin vadiler de vardır; ortaya çıkan grafiğin ortalaması ise sıfıra yakındır. Bu, 5 frekansının orijinal fonksiyona katkıda bulunmadığını gösterir.
Fourier dönüşümü bunu tüm olası frekanslar için yapar; orijinal fonksiyonu hem sinüs hem de kosinüs dalgalarıyla karşılaştırır (pratikte bu karşılaştırma, gerçek ve sanal sayıların birleşimini kullanarak karmaşık düzlemde gerçekleştirilir).
Bu yolla Fourier dönüşümü, ilk bakışta karmaşık görünen bir fonksiyonu yalnızca birkaç sayıya indirger. Bu da onu matematikçiler için önemli bir araç hâline getirir: Bir problemle karşılaştıklarında, onu dönüştürmeyi denerler; çoğu zaman problem, frekans diline çevrildiğinde çok daha basit hâle gelir.
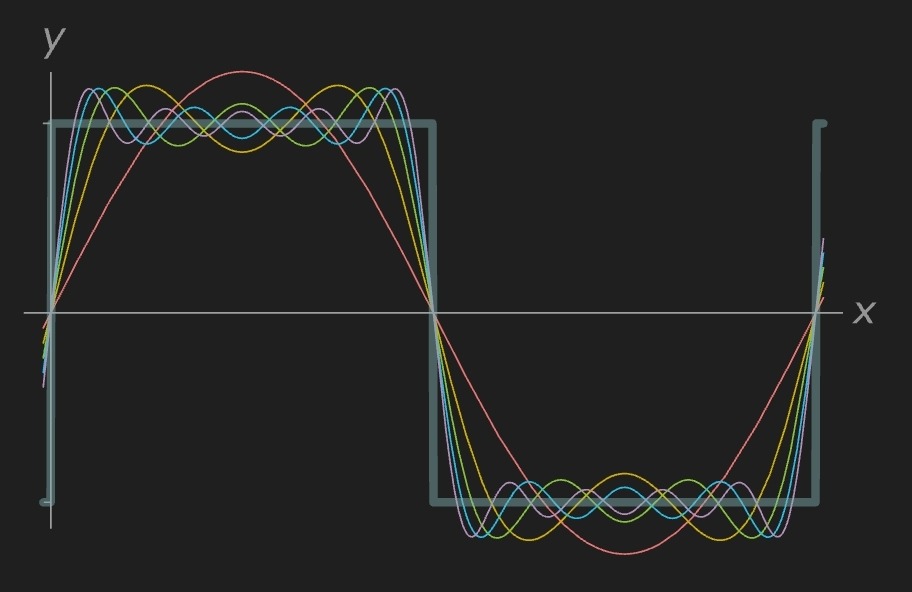
Eğer orijinal fonksiyon—genellikle dijital sinyallerde bulunan kare dalga gibi—keskin bir kenara sahipse, Fourier dönüşümü toplandığında bu kenara mümkün olduğunca yaklaşan sonsuz bir frekans kümesi üretir. Bu sonsuz kümeye Fourier serisi denir ve matematikçilerin başlangıçtaki tereddütlerine rağmen, günümüzde fonksiyon analizinde vazgeçilmezdir.
Çeviren: Arda Arpacı
Redaktör: Ayşe Yılmaz
Bilimsel Redaktör: Yasemin Poyraz Koçak