Geleneksel kuantum mekaniğinde geçmiş ve gelecek birbirine sıkı sıkıya bağlıdır. Belki de çok sıkı. Teoride yapılacak bir değişiklik, uzay genişledikçe kuantum olasılıklarının artmasına izin verebilir.
Uzayın genişlemesi, parçacıklara nerede olacakları konusunda giderek artan seçenekler sunarak kuantum mekaniği için sorun yaratmaktadır.
Modern fizikte şaşırtıcı bir bölünme yaşandı. Bir tarafta atom altı parçacıkları olasılıksal dalgalar olarak tasvir eden kuantum teorisi yer almakta, diğer tarafta izafiyet teorisi. Einstein’in yer çekimi sebebiyle uzay-zaman dokusunun büküldüğü fikri. Fizikçiler 90 yıldır kuantum mekaniğini ve yer çekimini kapsayan daha temel bir model oluşturmaya çalışıyor ama bu arayış birçok paradoksla karşılaştı.
Bu problemlerin en azından bir kısmı kuantum mekaniğinin merkezinde yer alan bir ilkede, nasıl işlediğine dair sorgulamak şöyle dursun, ifade edilmeye bile değmeyecek kadar açık görünen bir varsayımda yattığına dair ipuçları artıyor.
İlke olarak adlandırılan üniterlik, bir şeyin her zaman gerçekleştiğini söyler. Parçacıklar etkileşime girdiğinde tüm olası sonuçların olasılığı %100’e ulaşmalıdır. Bu gereklilikler, kuantum mekaniğinde kullanılan formülleri türetirken fizikçilere uzun zamandır rehberlik etmektedir. Illinois Üniversitesinde Yar. Doç. olan Yonatan Kahn, “İlk bakışta biraz önemsiz gibi görünse de bu çok kısıtlayıcı bir durum.” diyor.
Ancak bir zamanlar önemli bir köprü gibi görünen şey, fizikçilerin kuantum mekaniği ile yer çekimini uzlaştırmasını engelleyen boğucu bir deli gömleği haline gelmiş olabilir. Waterloo, Kanada’daki Perimeter Teorik Fizik Enstitüsünde teorisyen olan Bianca Dittrich, “Kuantum kütleçekiminde üniterlik çok açık bir sorudur.” dedi.
Asıl problem evrenin genişlemesi. Bu genişleme genel görelilik tarafından iyi tanımlanmıştır. Ancak bu, kozmosun geleceğinin geçmişinden tamamen farklı göründüğü anlamına gelirken üniterlik kuantum düzeyinde geçmiş ve gelecek arasında düzenli bir simetri gerektirir. Santa Barbara’daki California Üniversitesinde kuantum yer çekimi teorisyeni olan Steve Giddings, “Burada bir gerilim var ve eğer düşünürseniz bu oldukça şaşırtıcı bir şey.” dedi.
Bu çatışma konusundaki endişeler yıllardır devam etmektedir. Ancak son zamanlarda, iki kuantum yer çekimi teorisyeni, büyüyen kozmosumuza daha iyi uyması için üniterliğin tokalarını gevşetmenin bir yolunu bulmuş olabilir. Harvard Üniversitesinden Andrew Strominger ve Jordan Cotler, izometri adı verilen daha rahat bir ilkenin genişleyen bir evrene uyum sağlayabileceğini ve aynı zamanda üniterliği yol gösterici bir ışık haline getiren katı gereklilikleri karşılayabileceğini savunuyorlar.
“Üniterliğeihtiyacınız yok.” dedi Strominger. “üniterlik çok güçlü bir koşul.”
Birçok fizikçi izometri önerisine sıcak bakıyor, hatta bazıları bağımsız olarak benzer sonuçlar elde etmiş gözüküyor. Güncellemenin çok radikal olup olmadığı ya da yeterince radikal olup olmadığı konusunda görüşler farklılık göstermektedir.
Sabit Bir Tutar
Günlük hayatta, olaylar ister istemez tek bir şekilde gerçekleşir. Örneğin bir yazı tura atışının tura ya da yazı gelme ihtimali %100’dür.
Ancak bir asır önce, kuantum mekaniğinin öncüleri şaşırtıcı bir keşif yaptılar. Üniterliği sağduyudan kutsal bir ilkeye yükselten bir keşif. Sonuç tamamen sürprizdi. Matematiksel olarak kuantum dünyasının olasılıklarla değil, genlik olarak bilinen daha karmaşık sayılarla işlediğiydi. Bir genlik esasen bir parçacığın belirli bir durumda olma derecesidir. Pozitif, negatif veya karmaşık bir sayı olabilir. Bir parçacığı belirli bir durumda gözlemleme olasılığını hesaplamak için fizikçiler genliğin karesini alırlar. (Ya da genlik hayali bir sayı ise mutlak değerinin karesini alırlar.) Bu da hayali ve negatif bitlerden kurtulur ve pozitif bir olasılık üretir. üniterlik, bu olasılıkların toplamının-aslında tüm genliklerin karelerinin 1’e eşit olması gerektiğini söyler.
İşte bu bükülme – gerçekte gördüğümüz sonuçları hesaplamak için gizli genliklerin karesinin alınması – üniterliğe güç kazandırır. Bir parçacığın durumu değiştikçe, örneğin manyetik bir alandan geçerken veya başka bir parçacıkla çarpışırken genlikleri de değişir. Fizikçiler, bir parçacığın nasıl gelişmesine veya etkileşmesine izin verildiğini hesaplarken genliklerin asla karelerinin sabit toplamını bozacak şekilde değişmediği gerçeğini kullanırlar. Örneğin 1920’lerde bu üniterlik gereksinimi, İngiliz fizikçi Paul Dirac’ı antimaddenin varlığını ima eden bir denklem keşfetmeye yönlendirdi. Dirac, üniterliğe atıfta bulunarak “Sevgilime uymayacak herhangi bir teoriyi düşünmekle ilgilenmiyordum.” diye yazdı.
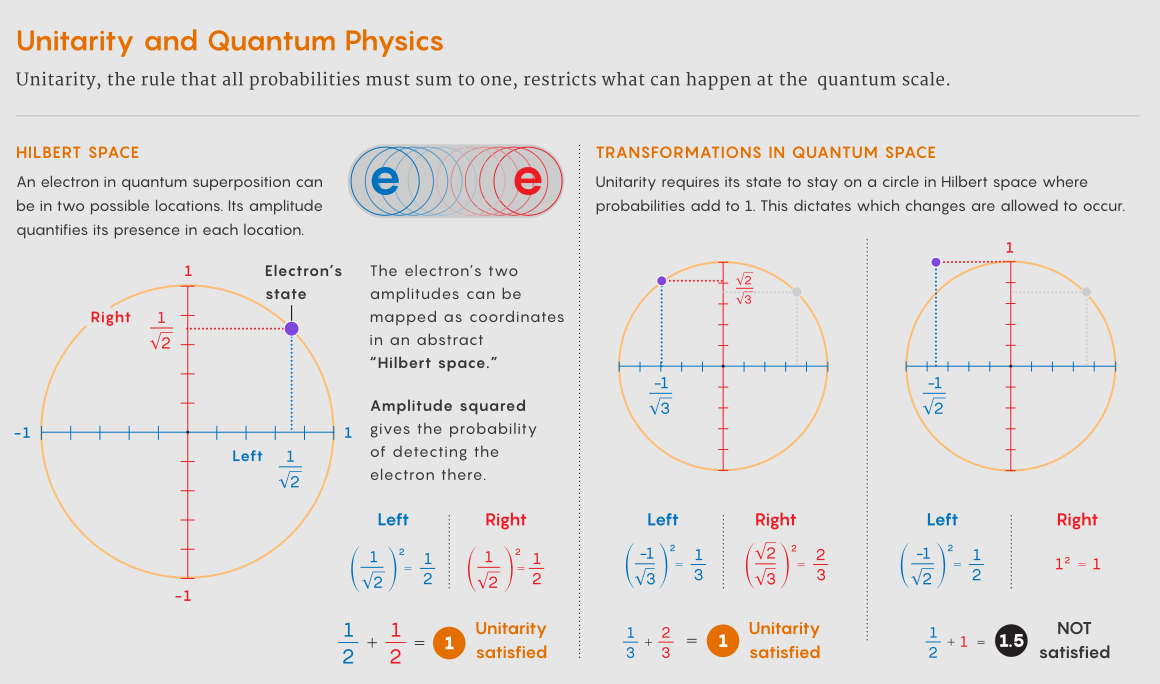
Fizikçiler, bir parçacığın kuantum durumunun Hilbert uzayında nasıl hareket ettiğini izleyerek olasılıkları ve genlikleri aynı hizada tutarlar. Parçacık için mevcut tüm olası durumları temsil eden soyut bir uzay. Parçacığın genlikleri Hilbert uzayındaki koordinatlarına karşılık gelir ve fizikçiler parçacıktaki değişiklikleri, koordinatlarını dönüştüren matris adı verilen matematiksel araçlarla bulur. Üniterlik, fiziksel olarak izin verilen bir değişikliğin, parçacığın Hilbert uzayındaki durumunu, koordinatlarının karelerinin toplamının 1’e eşit olmasını değiştirmeden döndüren özel bir “üniter” matrise karşılık gelmesi gerektiğini belirtir.
Bu felsefi sonuçları olan matematiksel bir gerçektir. Zaman içindeki bazı değişimlere karşılık gelen belirli üniter matrisi biliyorsanız herhangi bir kuantum durumu geleceğe döndürülebilir veya geçmişe döndürülebilir. Hilbert uzayında her zaman, asla büyümeyen veya küçülmeyen başka bir uygun duruma inecektir. Cotler, “Geçmiş tamamen geleceği, gelecek de tamamen geçmişi belirler.” dedi. “Bu, bilginin ne yaratıldığı ne de yok edildiği ifadesiyle ilgilidir.”
Yine de bu temel varsayım bizi çevreleyen evrenle çelişiyor gibi görünüyor.
Kozmik Bir Çatışma
Galaksiler birbirinden giderek uzaklaşıyor. Genişleyen evrenimiz genel görelilik denklemleri için tamamen geçerli bir çözüm olsa da fizikçiler giderek artan bir şekilde büyümesinin kuantum mekaniği için sorun yarattığını, parçacıklara nerede olacakları ve nasıl davranacakları konusunda genişleyen bir seçenek yelpazesi sunduğunu fark ettiler. Uzay büyüdükçe Hilbert olasılıklar uzayı da onunla birlikte nasıl büyümeyebilir? New Jersey Princetondaki İleri Araştırmalar Enstitüsünde teorik fizikçi olan Nima Arkani-Hamed, “Şu anki evrende, evrenin ilk zamanlarına göre daha fazla serbestlik derecesi olduğu kesinlikle doğru.” dedi.
Strominger, “Uzun yıllar boyunca bunun odadaki fil olduğunu hissettim.” dedi.

Miguel Montrero
Giddings, hem üniter hem de genişleyen bir evrende geçen paradoksal bir düşünce deneyiyle konuyu keskinleştiriyor. Evrenin şu anki durumunu alıp belki de burası ile Andromeda Galaksisi arasında yeni yaratılmış uzayda bulunan “zararsız bir foton” eklediğinizi düşünün diyor. Üniterlik; bu evrenin geçmişte neye benzediğini hesaplayabilmemiz, kuantum durumunu istediğimiz kadar değiştirebilmemiz gerektiğinde ısrar eder.
Ancak evrenin durumunu geri sarmak artı fazladan bir foton bir aksaklık yaratır. Geçmişe doğru gidildikçe evren ve fotonların dalga boyu da küçülür. Evrenimiz için bu bir sorun değildir. Bir foton sadece atom altı bir süreçle yaratıldığı ana kadar küçülür. Bu sürecin tersine çevrilmesi onu yok edecektir. Ancak fazladan foton bu özel süreçle yaratılmamıştır. Bu nedenle zamanı geri döndürdüğünüzde yok olmak yerine, dalga boyu sonunda inanılmaz derecede küçülecek ve enerjisini o kadar yoğunlaştıracaktır ki foton bir kara deliğe çökecektir. Bu durum bir paradoks yaratmakta ve saçma bir şekilde - bu kurgusal, genişleyen evrende - mikroskobik kara deliklerin fotonlara dönüştüğünü ima etmekte. Düşünce deneyi, üniterlik ve kozmik genişlemenin naif bir karışımının işe yaramadığını göstermektedir.Dittrich, üniterliğin daha genel sebeplerle şüpheli olduğunu düşünüyor. Kuantum mekaniği zamanı mutlak olarak ele alır ancak genel görelilik saatlerin tik taklarıyla oynayarak bir andan diğerine değişim kavramını karmaşıklaştırır. “Ben şahsen hiçbir zaman üniterliğe bu kadar güvenmemiştim.” dedi.
Asıl soru şu: Ne tür bir alternatif çerçeve hem kozmik genişlemeyi hem de kuantum teorisinin katı matematiğini barındırabilir?Üniterlik 2.0
Geçen yıl Strominger, zamanını kuantum yer çekimi araştırmaları ve kuantum bilgi teorisi - kuantum durumlarında depolanan bilgilerin incelenmesi - arasında paylaştıran Cotler ile bir işbirliği başlattı. İkili, kuantum bilgi teorisinde genişleyen evrene benzeyen iyi çalışılmış bir şema olduğunu fark etti: Kuantum hata düzeltme. Kuantum durumlarından yapılan küçük bir mesajın daha büyük bir sistem içinde gereksiz yere kodlandığı bir şema belki olabilir diye düşündüler. Genç evrenin içeriği benzer şekilde modern kozmosun şişmiş formuna işlenmiştir. Strominger, “Geriye dönüp baktığımızda bunun kuantum kodlama yapan insanların tam olarak yaptığı şey olduğu açık.” dedi.
Bu yılın başlarında yayınlanan bir makalede ikili, kuantum hata düzeltme kodlarının ait olduğu ve izometri olarak bilinen bir dönüşüm sınıfına odaklandı: İzometrik bir değişim. Daha fazla esnekliğe sahip üniter bir değişime benzer.

Gabriela Secara/Perimeter Enstitüsü
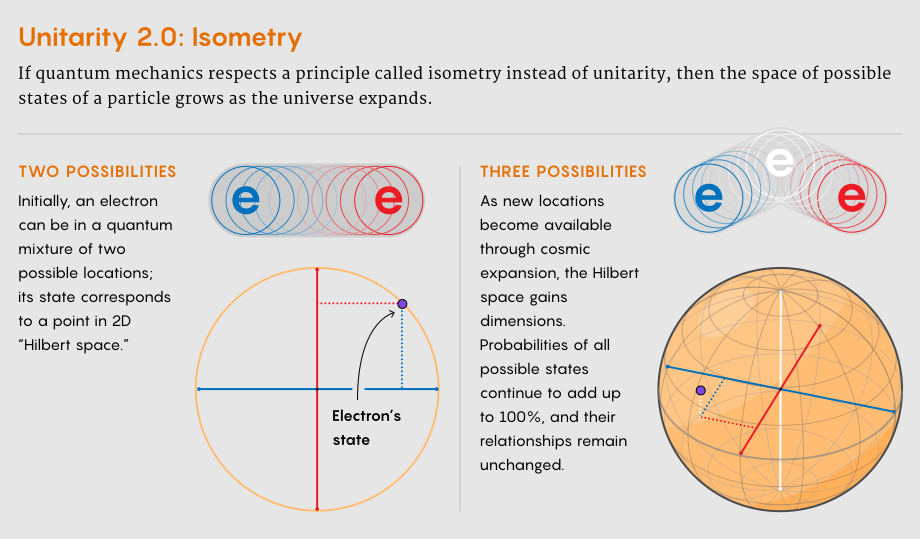
İki olası konumda bulunabilen bir elektron düşünün. Hilbert uzayı, iki konumdaki genliklerin tüm olası kombinasyonlarından oluşur. Bu olasılıklar bir daire üzerindeki noktalar olarak düşünülebilir. Her noktanın hem yatay hem de dikey yönde bir değeri vardır. üniter değişiklikler durumları daire etrafında döndürür ancak olasılıklar kümesini genişletmez veya daraltmaz.
Yine de izometrik bir değişimi görselleştirmek için bu elektronun evreninin üçüncü bir konuma izin verecek kadar şişmesine izin verin. Elektronun Hilbert uzayı büyür ama özel bir şekilde başka bir boyut daha kazanır. Daire, parçacığın kuantum durumunun her üç konumun karışımlarını barındırmak için etrafında dönebileceği bir küre haline gelir. Daire üzerindeki herhangi iki durum arasındaki mesafe, üniterliğin bir başka gerekliliği olan değişim altında sabit kalır. Kısacası, seçenekler artar; ancak fiziksel olmayan sonuçlar doğurmaz.
Giddings, “İzometrilerle çalışmak, üniterliğin bir tür genelleştirilmesidir.” dedi. “Özün bir kısmını koruyor.”
Evrenimiz, gerçek uzay genişledikçe sürekli çoğalan birçok boyuta sahip bir Hilbert uzayına sahip olacaktır. Kavramın daha basit bir kanıtı olarak Strominger ve Cotler, uzaklaşan bir aynada sonlanan bir çizgiden oluşan oyuncak bir evrenin genişlemesini inceledi. Evrenin bir uzunluktan diğerine büyüme olasılığını hesapladılar.
Bu tür hesaplamalar için kuantum uygulayıcıları genellikle bir kuantum sisteminin zaman içinde nasıl geliştiğini tahmin eden Schrödinger denklemini kullanırlar. Ancak Schrödinger denklemi tarafından dikte edilen değişiklikler tamamen tersine çevrilebilir. Arkani-Hamed, “Hayattaki gerçek amacı üniterliği sağlamaktır.” dedi. Bunun yerine Strominger ve Cotler, Richard Feynman tarafından oluşturulan ve yol integrali olarak adlandırılan alternatif bir kuantum mekaniği versiyonu kullandılar. Bir kuantum sisteminin bir başlangıç noktasından bir bitiş noktasına kadar izleyebileceği tüm yolların çetelesini tutmayı içeren bu yöntem, yeni durumların (birden fazla bitiş noktasına giden dallanma yolları olarak görünen) yaratılmasını karşılamakta sorun yaşamaz. Sonunda, Strominger ve Cotler’in yol integrali, oyuncak kozmosun büyümesini kapsayan bir matris ortaya çıkardı ve bu gerçekten de üniter bir matristen ziyade izometrik bir matristi. Cotler, “Eğer genişleyen bir evreni tanımlamak istiyorsanız Schrödinger denklemi bu haliyle işe yaramayacaktır” dedi. “Ancak Feynman formülasyonunda, kendi iradesiyle çalışmaya devam eder.” Cotler, izometriye dayalı bu alternatif kuantum mekaniği yönteminin “genişleyen bir evreni anlamamızda bize daha faydalı olacağı” sonucuna varıyor.
Bir Olasılıklar Serabı
Üniterliğin gevşetilmesi, Giddings ve diğerlerini rahatsız eden düşünce deneyindeki aksaklıkları çözebilir. Bunu da geçmiş ile gelecek arasındaki ilişkiyi ve evrenin hangi durumlarının gerçekten mümkün olduğunu nasıl düşündüğümüzü kavramsal olarak değiştirerek yapacaktır.
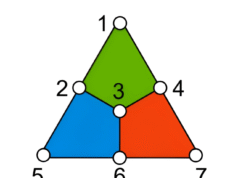
İzometrinin sorunu neden çözdüğünü görmek için Cotler, 0 veya 1-iki boyutlu bir Hilbert uzayı- olmak üzere iki olası başlangıç durumundan birinde doğan bir oyuncak evren tanımlar. Bu evrenin genişlemesini yönetmek için izometrik bir kural oluşturur. Birbirini izleyen her anda, her 0.01 olur ve her 1, 10 olur. Evren 0’da başlarsa ilk üç anı aşağıdaki gibi büyüyecektir: 0 → 01 → 0110 → 01101001 (8 boyutlu bir Hilbert uzayı). 0’ların ve 1’lerin süperpozisyonlarından oluşan çok daha uzun bir sicim muhtemelen gerçek evreni tanımlamaktadır.
Herhangi bir zamanda, oyuncak evrenin iki olası durumu vardır: Biri 0’dan, diğeri 1’den kaynaklanır. Başlangıçtaki bir basamaklı konfigürasyon daha büyük, sekiz basamaklı bir duruma kodlanmıştır. Bu yapı, başlangıçta iki ve sonda iki olasılık olması bakımından üniter bir yapıya benzemektedir. Ancak izometrik yapı genişleyen evreni tanımlamak için daha güzel bir çerçeve sağlıyor. Daha da önemlisi bunu, örneğin burası ile Andromeda arasına fazladan bir foton ekleme özgürlüğü yaratmadan yapıyor ki bu da zamanı geri çevirdiğinizde sorun yaratacaktır. Örneğin evrenin 01101001 durumunda olduğunu düşünün. İlk 0’ı 1’e çevirin – ekstra foton gibi küçük yerel bir değişikliği temsil eder – ve daha büyük Hilbert uzayında görünüşte geçerli bir koordinat kümesi ile kağıt üzerinde iyi görünen bir durum (11101001) elde edersiniz. Ancak belirli izometrik kuralı bildiğinizde, böyle bir durumun ana durumu olmadığını görebilirsiniz. Bu hayali evren asla ortaya çıkamazdı.
Cotler, “Geçmişte hiçbir şeye karşılık gelmeyen bazı gelecek konfigürasyonları var,”, “Geçmişte bunlara dönüşebilecek hiçbir şey yok.” dedi.
Giddings, geçen yıl kara delikler üzerinde çalışırken karşılaştığı paradoksal durumları elemek için benzer bir ilke önerdi. Buna “tarih önemlidir” diyor ve evrenin belirli bir durumunun ancak çelişkiler yaratmadan geriye doğru evrilebiliyorsa fiziksel olarak mümkün olduğunu savunuyor. “Bu uzun süredir devam eden bir bilmeceydi” dedi. Strominger ve Cotler “bu bulmacayı ele alıyor ve muhtemelen yeni bir düşünme biçimini motive etmek için kullanıyorlar.”
Giddings bu yaklaşımın daha da geliştirilmeyi hak ettiğini düşünüyor. On yıl önce iş arkadaşı Philipp Höhn ile birlikte uzay-zamanın pek önemsenmeyen bir kuantum teorisini formüle etmeye çalışırken izometri hakkında benzer farkındalıklara ulaşan Dittrich de öyle. Bir umut, bu tür çalışmaların sonunda evrenimizi yönetebilecek belirli bir izometrik kurala yol açabileceğidir. “0, 01’e gider” den daha karmaşık bir reçete. Cotler’a göre gerçek bir kozmolojik izometri, gökyüzündeki madde dağılımında hangi spesifik modellerin mümkün olup hangilerinin olmadığını hesaplayarak ve ardından bu tahminleri gözlemsel verilerle test ederek doğrulanabilir. “Eğer daha yakından bakarsanız bunu bulursunuz ama bunu bulamazsınız.” dedi. “Bu gerçekten faydalı olabilir.”
İzometri ve Ötesi
Üniterliğin gıcırtılı göründüğü bir düşünce deneyi, uzay-zamanı bir çıkmaz sokağa dönüştüren yoğun madde konsantrasyonları olan kara deliklerle ilgilidir. Stephen Hawking 1974’te kara deliklerin zamanla buharlaşarak içine düşen her şeyin kuantum durumunu sildiğini hesapladı. Kara delik bilgi paradoksu olarak bilinen görünüşte bariz bir üniterlik ihlali. Eğer kara delikler, Cotler ve Strominger’in varsaydığı gibi izometrik olarak olgunlaşan Hilbert uzaylarına sahipse, fizikçiler düşündüklerinden biraz daha farklı bir bulmacayla karşı karşıya kalabilirler. Strominger, “Bunu hesaba katmayan bir çözüm olabileceğini sanmıyorum.” dedi.
Bir başka ödül de, sadece evrenin nasıl büyüdüğünü değil, her şeyin ilk etapta nereden geldiğini de açıklayan ayrıntılı bir kuantum teorisi olacaktır. Arkani-Hamed, “Evrenimiz yoktu ve birdenbire bir evrenimiz oldu.” dedi. “Bu nasıl bir üniter yapıdır böyle?”.
Ancak Arkani-Hamed, izometriyi üniterlikle değiştirmenin yeterince ileri gittiğinden şüphe ediyor. Kendisi sadece üniterlik değil, kuantum teorisi ve genel görelilikteki birçok temel varsayımdan kurtulmaya çalışan bir araştırma programının liderlerinden biridir.
Bundan sonra hangi teori gelirse gelsin. Tıpkı kuantum mekaniğinin Isaac Newton’un hareket yasalarından temiz bir kopuş olması gibi tamamen yeni bir biçim alacağından şüpheleniyor. Yeni bir formun neye benzeyebileceğinin açıklayıcı bir örneği olarak, 2014 yılında o zamanki öğrencisi Jaroslav Trnka ile birlikte yaptığı bir keşiften kaynaklanan bir araştırma programına işaret ediyor. Belirli parçacıklar çarpıştığında, olası her sonucun genliğinin, genlik olarak adlandırılan geometrik bir nesnenin hacmine eşit olduğunu gösterdiler. Nesnenin hacmini hesaplamak, bir parçacık çarpışmasının an be an gerçekleşebileceği tüm yolları zahmetli bir şekilde yeniden yapılandıran genlikleri hesaplamak için standart yöntemleri kullanmaktan çok daha kolaydır.
İlginçtir ki, genlik üniterliğe uyan cevaplar verirken prensip şeklin kendisini inşa etmek için kullanılmaz. Parçacıkların uzay ve zamanda nasıl hareket ettiğine dair herhangi bir varsayım da yoktur. Parçacık fiziğinin bu tamamen geometrik formülasyonunun başarısıdır. Şu anda çatışan aziz ilkelerden arınmış, gerçekliğe yeni bir bakış açısı olasılığını artırıyor. Araştırmacılar, farklı parçacıklara ve kuantum teorilerine ait ilgili geometrik şekilleri keşfetmek için bu yaklaşımı giderek genelleştirmektedir.
“Cotler, “Bu üniterliği organize etmenin farklı bir yolu olabilir ve belki de onu aşmak için tohumları vardır.” dedi.
Çevirmen: Emre Kollu
Redaktör: Erdal Eren Uğurcuklu









Yoruma kapalı.